La importancia de Los acuerdos en la política es de gran trascendencia en la economía de un país pues sin una cooperación entre las distintas fuerzas políticas se pueden estancar las reformas y acuerdos en beneficio de una mejor situación económica. Cuando existe desacuerdo en los parlamentos o cámaras y, por tanto, no hay un óptimo resultado en la formación de coaliciones, se puede llegar a crear inestabilidad e incertidumbre como lo fue el caso del 20 de diciembre de 2015 (20D) en España.1 Por otro lado, la trascendencia económica que tiene la estabilidad política al haber cooperación entre las distintas fuerzas políticas puede evitar incertidumbre a la hora de gobernar, de forma especial en los mercados y en algunas variables económicas, ya sea de forma directa o indirecta. Sin duda, muchas de las decisiones económicas de un país son discutidas en las Cámaras, por lo cual, el estudio de la forma en cómo son tomadas las decisiones en estos últimos es de gran trascendencia.2
Para la toma de decisiones y la aprobación de acuerdos, es importante que el partido en el poder cuente con los votos suficientes o que, en su defecto, tenga partidos aliados para poder rebasar ciertas cuotas de mayoría exigidas por la ley. En el caso de la Constitución mexicana, esta señala, en su artículo 135, que para ser reformada se requiere el voto de las dos terceras partes de los diputados y senadores, y que sean aprobadas por la mitad más una de las 32 Legislaturas lo cales de cada estado. Se esperaría que mientras mayor poder de decisión tenga un partido y sus aliados, mayor será su productividad en los parlamentos. Sin embargo, muchas veces los votos no son suficientes para aprobar ciertos acuerdos, y se tiene que recurrir a la formación de coaliciones con otras fuerzas políticas.
Desde la teoría económica y política, este tipo de tópicos pueden ser abordados por la nueva economía política (NEP).3 Algunas de las características de la NEP son: i) presupone la elección racional de los agentes; ii) el comportamiento político es maximizar la utilidad de los agentes; iii) las políticas públicas son resultado de racionalidad e interacción entre agentes, y, iv) se utiliza un método deductivo. A grandes rasgos, siguiendo a Bonilla y Gatica (2005), la NEP se divide en las siguientes ramas: i) teoría espacial del voto (TEV);4 ii) teoría de juegos e información asimétrica aplicada a la competencia política, y, iii) ciclo político económico. De las dos primeras ramas es desde donde se puede abordar al análisis de estabilidad de coaliciones políticas, usando para ello distintos modelos de teoría de juegos.5
La teoría de juegos ofrece una metodología para el análisis de estabilidad de coaliciones de este tipo mediante el uso de determinados índices (o valores) de decisión. La manera en cómo esta teoría ha incursionado en este tipo de tópicos viene de mucho tiempo atrás. Se considera que la teoría de juegos comenzó con el trabajo de Neumann y Morgernstern (1944)). La teoría de juegos cooperativos (TJC)6 logró importantes resultados en las contribuciones de Nash (1953) y Shapley (1963) sobre los juegos de negociación, y las de Gillies (1953) y Shapley (1963) sobre el núcleo de un juego.7 Shapley, junto con otros autores posteriores, Shapley y Shubik (1954), y Banzhaf (1965), llevarían a cabo el desarrollo de soluciones distintas a la solución núcleo8 mediante propuestas de diferentes valores de poder de decisión9 dentro de un juego cooperativo.
El valor del índice de Shapley-Shubik (S-S) da como resultado una cantidad que representa la posible contribución de cada uno de los jugadores a las coaliciones de las que podría formar parte. Por su parte, el índice de poder de Banzhaf explica el papel de los votos decisivos para la toma de decisiones entre varios agentes. De tal manera, el trabajo de Leech (1990) sugiere que el índice S-S es más apropiado para situaciones en que los votos reflejan un conjunto común de valores y todos los posibles conjuntos de valores tienen el mismo peso (la distribución es uniforme). Así, el índice de Banzhaf es más apropiado si los votantes actúan de manera independiente uno del otro y no requieren el mismo rango de valores; lo único necesario en una situación promedio es que ellos conozcan la manera en que vota el otro. Existen otros trabajos que sugieren representaciones alternativas de los índices de S-S y de Banzhaf, que abundan más sobre ellos (véanse, Felsenthal y Machover 1996; Laruelle y Valenciano 2001; Chua y Huang 2003 y Kirsch y Langner 2010). Existen otros índices como el de Deegan-Packel (1979) y el de Holler-Packel (1983) basados en coaliciones mínimas ganadoras (CMGs), en las cuales cada votante es decisivo para lograr un objetivo.
Por otra parte, se han desarrollado valores coalicionales que incorporan dentro de los juegos cooperativos ciertas particiones10 del conjunto total de jugadores, dando lugar a estructuras de coalición de los diferentes jugadores.11 Dicha partición da lugar a que los jugadores obtengan valores de poder de decisión que incorpora su interacción con los miembros de su coalición y de las demás coali ciones. Los juegos con una estructura coalicional fueron considerados inicialmente en el trabajo de Aumann-Dreze (1974), en el cual se extiende al valor de Shapley, donde el juego original se divide en subjuegos, tantos como número de particiones se tenga del conjunto total de jugadores, y donde cada jugador recibe su equivalente al valor de Shapley de acuerdo con el subjuego (o partición) del cual forma parte. Después, en el trabajo de Owen (1977), se propuso una aproximación diferente donde se toma en cuenta tanto el poder de decisión de los jugadores dentro de la coalición de la cual se forma parte, como del poder de la coalición dentro del conjunto total de coaliciones. Para lo anterior, es necesario formular un juego cociente,12 el cual toma en cuenta el peso en votos de cada una de las coaliciones involucradas en el juego y el peso de cada uno de los jugadores individuales. A este valor se le suele llamar valor coalicional de Owen (VCO).
Existen otros valores alternativos al VCO como el que se propone en el trabajo de Owen (1981), donde usa el valor de Banzhaf para modificar la forma en que se valora a los jugadores que se interrelacionan. A dicho valor se le suele llamar valor de Banzhaf-Owen. Por su parte, en el trabajo de Alonso y Fiestras (2002) se introduce el valor de Banzhaf aplicado en la valoración del juego cociente y el valor de Shapley aplicado a las uniones de coaliciones.
En trabajos más aplicados, concretamente a política y donde se utilizan los valores de Shapley y/o de Owen, están los de Geddes (1991) donde se propone un modelo de teoría de juegos para intentar explicar los diferentes modos de transición hacia regímenes democráticos. El modelo de Geddes (1991) arroja dos predicciones: 1) es más probable que las reformas se aprueben cuando el poder se distribuye equitativamente entre los partidos más fuertes, y, 2) es más probable que las reformas iniciales sean seguidas de nuevas ampliaciones (leyes secundarias), si el peso electoral de la bancada permanece estable y relativamente estable. También se han usado los valores de poder para estudiar los parlamentos como es el caso de los trabajos de Carreras (1992), donde se hace un estudio coalicional de los parlamentos autonómicos españoles de régimen común y el de Carreras y Owen (1995), donde se estudia y aplica el valor coalicional en las estrategias parlamentarias españolas.
En el caso de México, trabajos como el de Nacif (2003) abordan modelos para explicar la creación y estabilidad de coaliciones entre los diferentes poderes y dentro del Congreso mexicano para legislar y crear proyectos de política pública. Nacif argumenta que los partidos políticos en los sistemas presidenciales tienen incentivos para cooperar y construir coaliciones para formular políticas públicas; su construcción dependerá de los beneficios que pueden obtener con la cooperación entre el partido del presidente y los partidos de oposición al modificar el status quo. Esta es otra forma de ver la importancia de formar coaliciones dentro de los parlamentos, tanto para los partidos en el poder como para los que no son parte de él. Ello puesto que ante un escenario cooperativo se puede lograr una buena productividad en políticas públicas, lo cual se espera sea benéfico para el partido gobernante y traiga algún rendimiento para los otros partidos, ya sea de carácter político y/o económico. El modo en que el partido o coalición del gobierno logre el mayor número de políticas dependerá en parte del influyentismo que este tenga sobre los demás partidos o sobre las demás coaliciones políticas, es decir, en la forma en la cual puede impactar sobre la decisión de voto de los demás. En los congresos, esto se puede presentar en formas directas de voto como lo es la aprobación o rechazo de las distintas propuestas que presenten los diferentes partidos, o bien de maneras indirectas de voto como lo son la abstención y ausentismo.
Las situaciones de inestabilidad o incertidumbre generadas cuando los partidos políticos no llegan a acuerdos y, por tanto, posponen decisiones o toman decisiones subóptimas, en el sentido de Colomer (2001) en materia económica, han tenido lugar en el caso mexicano, lo cual ha sido analizado y documentado desde la primera situación de gobernanza de mando no unificado, que algunos llaman “gobierno dividido” (Nacif 2003; Negretto 2003), la cual surgió a partir de la LVII Legislatura (1997-2000), cuando el partido del presidente en turno o la coalición partidista que lo llevó a ese cargo no fue por sí misma mayoría absoluta en alguna o en ambas Cámaras del Congreso (Paoli Bolio 2012). Tal situación prevaleció a partir de la primera alternancia (2000), durante la segunda (2012) y hasta la tercera alternancia partidista en la presidencia (2018). Cuando se restablece la situación de gobierno unificado, un partido o una coalición partidista deciden por sí mismos en las Cámaras sin requerir de otros partidos o coaliciones, con excepción de aquellas decisiones cuya validez requiere de mayoría colegiada.
Así, el objetivo de la presente investigación es analizar el poder de decisión de los partidos políticos en las Legislaturas LXIII y LXIV mediante distintos índices teóricos de los juegos cooperativos y con el uso de simulaciones desarrolladas en SCIentific LABoratory (Scilab).13
Para lograr este objetivo se divide el trabajo de la siguiente manera: i) en un primer apartado, se presentan, de manera formal, los juegos de mayoría ponderada y los distintos índices (o valores) de poder más comunes (el valor de Sha pley-Shubik y de Banzhaf); ii) en una segunda sección, se abordan los valores coalicionales usados en la investigación (el valor coalicional de Owen y el valor de Aumann-Dreze) con el propósito de compararlos con los valores individuales de cada jugador; iii) en un tercer apartado, se hace el análisis del poder político de los partidos dentro de la LXIII y LXIV Cámara de Diputados, usando, para ello, los valores de poder discutidos con anterioridad, y, iv) finalmente, se presentan las conclusiones correspondientes.
En esta sección se discuten los principales conceptos para entender los juegos simples y ver los juegos de mayoría ponderada como un caso particular de los mismos. Así también, se presentan los principales índices de poder que se manejan en la literatura para medir el poder de decisión de los jugadores en los juegos simples.
Se comienza entonces por analizar dos de los valores más comunes en los juegos de negociación en la TJC: los valores de Shapley (Shapley-Shubik) y de Banzhaf, dando antes la definición de un juego cooperativo.
Juego cooperativo (Amer et al. 2003, 108): Un juego cooperativo es un par Γ ≡ (N, v), donde N es un conjunto de jugadores (también llamada gran coalición) y v ∶ 2N → ℝ es una función característica (donde 2N denota el conjunto potencia de N) el cual asigna a cada coalición de jugadores un pago o valor, con v(∅) = 0.
Índice de Shapley (IS) (Gilles 2010, 75): Sea Γ = (N, v) un juego cooperativo, con N = {1, 2, ..., n} el conjunto de jugadores y v su función característica. Denótese con S = {n1, n2, ..., nk }, 1 ≤ nj ≤ n, una coalición en N, con n = |N| y s = |S|. El índice de Shapley (IS) se define como:
En este índice de estabilidad14 se le da la misma probabilidad de ocurrencia a la formación de las coaliciones de tamaño s = |S| y donde
Así, Si es el valor esperado de la contribución marginal del jugador i cuando todos los órdenes de formación de la coalición son igualmente probables. Como se puede observar, dicho índice depende de las combinaciones del tamaño de las diferentes coaliciones de las que el jugador i puede formar, pero sin contarse a él mismo, por ello es que se considera n - 1Cs - 1.
Existen otras formas de presentación del valor de Shapley, como el que se muestra en Peleg y Sudholter (2007, 154) y en Gilles (2010, 72), además de otras formas más generales (como la formulación probabilística) que se puede consultar también en Gilles (2010, 75).
Índice de Banzhaf (IB) (Sánchez 1994, 103): En un juego cooperativo (N, v), como el de la definición anterior, para todo n existe una función β tal que:
A βi(v ) se le llama el índice de Banzhaf (IB) correspondiente al i-ésimo jugador.
Es importante señalar que, cuando se aplican a juegos de mayoría ponderada (definidos enseguida), el índice de Shapley es más apropiado cuando todos los jugadores tienen un valor común al juzgar una propuesta. Por su parte, el índice de Banzhaf se ajusta más cuando todos los jugadores tienen su propio valor al juzgar una propuesta determinada.
Juego cooperativo simple (JS) (Peleg y Sudholter 2007, 16-17): Un juego cooperativo simple o juego simple (JS) v, es aquel donde para toda coalición S ⊆ N se tiene que:
Todo juego simple (JS) está determinado por la colección de coaliciones ganadoras (W)15 como sigue:
Se puede deducir que N ∈ W y ∅ ∉ W en todo juego v ; además, si S ⊆ T y S ∈ W ⇒ T ∈ W.
Con base en la segunda observación, se puede acotar aún más al juego v considerando solo la colección de coaliciones mínimas ganadoras (Wm)16 como sigue:
Clasificación de JS (Peleg y Sudholter 2007, 17): Sea (N,v ) un JS con W su colección de coaliciones ganadoras. Se tiene entonces la siguiente clasificación.
El JS es propio si S ∈ W ⇒ N ∖ S ∉ W;
El JS es fuerte si S ∉ W ⇔ N ∖ S ∈ W;
El JS es débil si V = ∩S∈W S ≠ ∅;
El JS es dictatorial si ∃ j ∈ N tal que S ∈ W ⇔ j ∈ S.
A los miembros de v en el caso 3) de la definición anterior se les denomina jugadores con veto y al jugador j en el caso 4) se le llama dictador.
Juego de mayoría ponderada (JMP) (Peleg y Sudholter 2007, 17): Un juego de mayoría ponderada (JMP) es un caso particular de un juego simple. El juego v es de mayoría ponderada si existe una distribución de pesos w1, w2, ..., wn entre los jugadores y una cantidad de mayoría o cuota (q) tales que:
con w(S) = ∑i∈Swi , ∀ S ∈ W.
Usualmente, un JMP se representa por v ≡ [q; w1, w2, ..., wn].
Índice de Shapley-Shubik (ISS) (Amer et al. 2003, 121): El índice de Shapley-Shubik (ISS) es el IS restringido a juegos simples para cada jugador i, i. e., es un índice SSi = Si | JS con las siguientes características:
Se puede dar una generalización del valor de Shapley mediante estructuras de coalición. En el valor coalicional de Owen se encuentra dicha generalización, del cual, a partir de un caso particular, se puede deducir el índice de Shapley. Se desarrolla a continuación dicho valor coalicional junto con el valor de Aumann-Dreze.
Como se trabajará con “estructuras de coaliciones” en N, se necesitará la definición de una “partición de un conjunto” y la definición de un “conjunto cociente”. Se explica esto enseguida, definiendo para ello algunos conceptos pertinentes:
Conjunto de índices (Munkres 2000, 25): Un intervalo o conjunto de índices es un conjunto finito o infinito de números naturales o reales y se denota como I.17
Partición de un conjunto (Munkres 2000, 23): Sea A ⊆ ℝn un conjunto no vacío. Una partición P del conjunto A es una familia de subconjuntos que cumple lo siguiente:
P = {Ai : i ∈ I }, para algún intervalo I,
∀ i ∈ I, Ai A y Ai ≠ ∅,
∀ i ≠ j, Ai ∩ Aj = ∅,
Ejemplo: sea A como en la Figura 1.
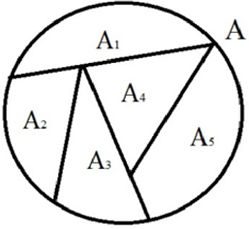
El conjunto finito A está formado por los subconjuntos Aj , j = 1, ..., 5.
Fuente: Elaboración propia.
En este ejemplo se tiene que:
P = {Ai : i ∈ I}, con I = {1, 2, 3, 4, 5},
A1,...,A5 ⊆ A, Aj ≠ ∅,
A1 ∩ A2 = ∅ ,...,A4 ∩ A5 = ∅,
Número de particiones de un conjunto (Rota 1964, 500): Sea A un conjunto finito y n = |A|, es decir A es de la forma: A = {a1 ,..., an}. Al número de particiones de A (o equivalentemente el número de relaciones de equivalencia en el mismo) se le llama el número de Bell.18 Comenzando con B0 = B1 = 1, los números de Bell satisfacen la siguiente fórmula recursiva:19
Ejemplo: el conjunto A = {1, 2, 3} tiene 5 particiones posibles: P1 = {A1, A2, A3} = {{1}, {2}, {3}}; P2 = {{1, 2}, {3}}; P3 = {{1, 3}, {2}}; P4 = {{1}, {2, 3}}; P5 = {{1, 2, 3}}; ello coincide con el tercer número de Bell (B3) si se usa la forma recursiva anterior.
Relación de equivalencia (Shick 2007, 25-26): Sea K un conjunto, K ≠ ∅. Una relación binaria definida sobre K, R, es una relación de equivalencia si cumple con las siguientes propiedades:
a) Reflexibilidad: todo elemento x ∈ K está relacionado consigo mismo, i. e.: ∀ x ∈ K ⇒ xRx.
b) Simetría: si un elemento de K está relacionado con otro, ese otro también
está relacionado con el primero, i. e.: ∀ x, y ∈ K, si xRy ⇒ yRx.
c) Transitividad: si un elemento está relacionado con otro y este con un tercero, entonces el primero y el tercero también lo están, i. e.: ∀ x,y,z ∈ K: xRy ∧ yRz ⇒ xRz.
Notación: Una relación de equivalencia (∼) sobre K se denota como: (K,∼).
Clase de equivalencia (Shick 2007, 26): Dado un elemento a ∈ K, el conjunto dado por todos los elementos relacionados con a define la clase:
A la relación (1) se le llama la clase de equivalencia asociada con el elemento α y a α se le denomina representante de la clase.
Se puede observar que R define subconjuntos disjuntos20 en K, dichos subconjuntos son precisamente las clases de equivalencia. Al número de clases que genera una relación de equivalencia se le llama el orden de la clase y si este es finito, se dice que R es de orden finito.
Conjunto cociente (Shick 2007, 27): Al conjunto de todas las clases de equivalencia se le denomina conjunto cociente y se suele denotar como: K/R o K/∼.
Nota: se puede ver a K/R como un conjunto de subconjuntos: K/R = {[a1], ..., [ak]}.
Se puede demostrar que una relación de equivalencia R sobre un conjunto K ≠ ∅ induce una partición de este, y una partición de K determina una relación de equivalencia en este.
Ejemplo de relaciones de equivalencia: la igualdad matemática en K = R. Esta igualdad se puede escribir como: aRb ⇔ a - b = 0 ⇔ a = b.
Es así como se han presentado los conceptos necesarios para definir a los valores coalicionales.
Estructura de coaliciones (Carreras 1992, 5): Una estructura de coaliciones en N es una partición de la forma: B ≡ {N1, N2, ..., Nm}, donde m ≤ n = |N| y con:
Con esta definición basta para presentar al primer valor coalicional.
Valor de Aumann-Dreze (VAD) (Parilina y Sedakov 2015, 4-5): Dada la estructura de coaliciones B ≡ {N1, N2, ..., Nm}, para cada jugador i ∈ N se define el valor de Aumann-Dreze (VAD) como sigue:
donde se retoman los valores que arroja la función característica v (respecto a un JMP, por ejemplo) y donde B(i) es aquella coalición Nj tal que contiene al jugador i.
El VAD cumple con los mismos axiomas que el valor de Shapley, pero donde la eficiencia
es relativa, pues para cada estructura de coalición de la forma B ≡ {N1, N2, ..., Nm}, se tiene que
Para el segundo valor coalicional se define tanto el conjunto como el juego cociente.
Conjunto cociente (Carreras 1992, 5): Definiendo a j como el representante de Nj, j = 1, 2,..., m, se define al conjunto cociente de N con respecto a la partición (o relación de equivalencia) B, como:
En la última igualdad se hace un abuso de notación, por lo pronto se hace solo para simplificar al conjunto cociente y para que se obtenga algo congruente con las definiciones posteriores.22
Juego cociente (JC) (Carreras 1992, 5): Dado un juego v sobre N, el juego cociente (JC) vB sobre M se define por:
Proposición (Carreras 1992, 5):
Si v es simple ⇒ vB es simple. Si v es de mayoría ponderada ⇒ vB es de mayoría ponderada.
Demostración:
Se sigue que, al ser M formado por elementos de N, se heredan las propiedades de v, ya sea éste un juego simple o de mayoría ponderada.
Sea GN el conjunto de todos los juegos posibles en N (todos los v’s posibles). Sea BN el conjunto de todas las estructuras de coaliciones en N (todas las B’s posibles). El valor coalicional es la única aplicación: ϕ∶ GN × BN → ℝn, que asocia a cada juego v sobre N y a cada estructura de coaliciones B en N un vector de la forma:
y que satisface los siguientes axiomas:
1) Eficiencia. Para toda B ∈ BN:
a)
b) ϕi (v ; B) = 0, ∀ jugador i nulo en v.
2) Simetría. Si los jugadores i y k son indiferentes en v y pertenecen a la misma subcoalición23 Nj, entonces:
3) Simetría en el cociente. Si j y h son indiferentes en el juego cociente vB, entonces:
4) Aditividad. Para todo v, v’ ∈ GN y para toda B ∈ BN:
Una fórmula explícita del valor coalicional es la propuesta por Owen (1977), dada en la siguiente definición:
Valor coalicional de Owen (VCO) (Carreras 1992, 6): Sea N ∈ GN, B ∈ BN una partición de N y M el conjunto cociente de B con las definiciones explícitas de estos conjuntos antes expuestas. Si i ∈ Nj entonces:
donde j ∉ H ⊆ M, i ∉ K ⊆ Nj, Q = ⋃r∈HNry m, h, k y nj son los cardinales respectivos de M, H, K y Nj. A cada valor ϕi se le denomina el valor coalicional de Owen (VCO) para el i-ésimo jugador.
Es importante señalar que en la definición anterior se debe considerar al conjunto vacío tanto para K como para H (y por tanto para Q). Además, si solo existe una subcoalición N1, la forma en que se debe tomar a B es la siguiente: B = {J1, J2, J3, ..., Jm} donde Js, s = 2, ..., m, son los jugadores que no están contemplados en N1 los cuales van en coalición unitaria; por supuesto, puede haber más de una coalición no unitaria (más de una N1). En todos los casos se debe poner a M de la forma: M = {1, ..., m} para que la unión de subcoaliciones en Q sean las correctas.24
Entonces, ϕi es el valor esperado de la contribución marginal del jugador i cuando solo se consideran, con igual probabilidad, los órdenes de formación de la coalición total en los que aparecen juntos los miembros de cada Nr para r = 1, 2, ..., m.
Se trata así de una analogía con el valor de Shapley (en particular con la forma presentada en la ecuación (2) solo que se hace en dos partes: i) valoración local (VL), donde se valora a cada jugador i de forma local, dentro de su subcoalición correspondiente (su Nj) y que se ve reflejado en la parte de las K’s, y, ii) valoración global (VG), donde se muestra la valoración de cada subcoalición en una forma global dentro del juego cociente (dentro de M), es decir, donde se toma a cada Nj como jugador individual, cuya participación se representa en la parte de las H’s (y por consecuencia en las Q’s ). Así, la ecuación (2) puede dividirse de la siguiente manera:
Cuando la estructura de coaliciones es trivial, es decir, B = {N}, el valor coalicional se reduce al valor de Shapley. Lo anterior puede comprobarse de manera sencilla si se hacen las simplificaciones correspondientes en la ecuación (2) con la estructura B = {N}. En este caso la VL de cada jugador i es sobre sí mismo y la VG de cada Nj (que es igual a j) se hace sobre el conjunto M = N.
Autores como Carreras (1992) coinciden en que mediante la interpretación probabilística del valor coalicional no debe haber dificultad en extenderlo a estructuras de orden superior en el caso de que alguna Nj ∈ B contenga a, su vez, una subestructura de coaliciones. En este sentido el proceso puede continuar “hacia el interior” con la única limitación de la indivisibilidad de los jugadores en el juego original.
Cuando se aplica el valor coalicional a un juego simple, se obtienen resultados en porcentajes (análogo al ISS) solo que en este caso no tiene algún nombre en específico. Este tipo de estructuras de coalición se utilizan en juegos más dinámicos como lo son los juegos estocásticos (véase, por ejemplo, Parilina y Sedakov (2015)).
Para finalizar esta primera parte del trabajo, en la Tabla 1 se presentan las ventajas y desventajas de los índices de poder abordados.25
En esta sección se analiza el poder de decisión de los partidos políticos dentro de las Legislaturas LXIII y LXIV de la Cámara de Diputados (en adelante CdD) usando la teoría de los valores de poder vistos en la sección anterior.26 Estos casos de estudio se abordan desde un enfoque interdisciplinario, pues, desde sus bases teóricas inmersas en la NEP, se considera que es una rama interdisciplinaria de la economía, en el entendido de que necesita de la ciencia matemática, económica y política, para su óptimo desarrollo y análisis (Bonilla y Gatica 2004).27
En este primer caso de estudio, se hace una comparación del poder de decisión de los partidos que formaron parte de la reciente LXIII CdD.28 En la primera parte, se presentan los valores individuales de poder de decisión que tienen los partidos por sí solos, es decir, sin hacer coaliciones, y, en una segunda parte, sus valores coalicionales dados distintos escenarios, así como su comparación con alguno de los índices individuales. En ambos casos se usan códigos de programación desarrollados en Scilab para analizar los diferentes juegos.
Después de las elecciones del 2015, la LXIII CdD, comprendida del año 2015 al año 2018, quedó conformada de acuerdo con el Cuadro 1.
[i] Fuente: Elaboración propia con información del sitio http://www.diputados.gob.mx/.
Obsérvese que son tomados en cuenta nueve jugadores, donde el PRI tiene la primera posición en escaños, el PAN la segunda y el PRD la tercera. En esta Legislatura, MORENA (MRN, en adelante) se posicionaba apenas como quinta fuerza política; se menciona esto último puesto que para la siguiente Legislatura, MRN pasaría a ocupar la primera posición.
Como cuota (o umbral) del JMP, se decide usar la mayoría relativa calificada (o simplemente mayoría calificada), esto es, la necesaria para aprobar reformas constitucionales, representada por las dos terceras partes del total, es decir, de q = 334.29
Así, tomando en cuenta la cuota de mayoría anterior, el JMP para la LXIII Legislatura se escribe como:
Con ayuda de Scilab se pudo comprobar la existencia de 152 coaliciones ganadoras (CGs) en total, así como que el jugador 1 (el PRI) tuviera veto, pues todas las CGs necesitaban de él para ganar el JMP. No obstante, el conjunto de CMGs se reduce a solo 9, ello debido al poco peso de los partidos pequeños y a la concentración de poder en las tres primeras fuerzas políticas. Con el enumerado correspondiente de cada partido expuesto en el cuadro 1, el conjunto de CMGs es:
El ISS y el IB se presentan en el Cuadro 2.
Se observa que el ISS premia más al PRI y castiga más al PAN, si se compara con el IB. Si se fija en el ISS, el 75% del poder se reparte entre los dos partidos anteriores y tan solo el 25% del poder restante se reparte entre los otros 7 jugadores, los cuales obtienen un mayor poder con el IB. Al único candidato independiente se le otorga un índice de poder nulo. La segunda fuerza de la izquierda la desempeña MRN, este último partido sería fundamental en la reconfiguración de la Legislatura posterior.
Se analizan ahora algunos escenarios del juego cociente y sus respectivos valores coalicionales. Se presentan algunos casos donde las coaliciones se forman de manera “natural” y “no natural”, ello siguiendo una ideología determinada en el primer caso y coaliciones diversas en la segunda, donde no necesariamente los partidos en coalición son de la misma ideología.30
Como primera aproximación de un JC, se inicia de la partición B = {B C , B D , B I }, donde B I = {MC, PRD, MRN} es el bloque de la izquierda, B C = {PVEM, PRI, PANAL, IND} es el bloque del centro y B D = {PAN, PES} es el representante de la derecha. En adelante se refiere a dicha partición como la partición natural debido al carácter ideológico de B. En consecuencia, el JC derivado de dicha partición se denominará JC natural. Nótese que se ha considerado al candidato independiente dentro del centro, ello debido a la forma en como votó el candidato independiente durante gran parte del ejercicio de la LXIII CdD.
Tomando en cuenta esta partición, y con el enumerado correspondiente de cada partido (véase el Cuadro 1), el conjunto B del juego cociente es:
Usando la cuota q = 334 y el peso de cada partido (siguiendo el Cuadro 1) se tiene que: B = [334; 262, 118, 120].
Por medio de simulaciones desarrolladas en Scilab se presentan, en el Cuadro 3, los valores de Shapley-Shubik originales de cada jugador y los valores coalicionales de Aumann-Dreze y de Owen.31
Una primera observación de los valores coalicionales es que con el VAD todos los partidos tienen un valor nulo, ello puesto que todas las coaliciones formadas de manera natural no alcanzan en conjunto a rebasar la cuota de mayoría. Es por ello que, en lo subsiguiente, cuando se hable del juego o valor coalicional, se refiere particularmente al VCO, al menos que se especifique lo contrario.
Se tiene que, a excepción del diputado independiente, en el centro todos ganan con el juego coalicional y que el más beneficiado es el PANAL pues iguala en poder al PVEM. Caso contrario pasa en la derecha, donde ambos partidos de esa ideología pierden, el PAN pierde un 4% de poder y el PES se vuelve nulo en poder. Por su parte, en la izquierda, el más beneficiado es el PRD (aumenta un 2% su poder con el VCO) a costa de la pérdida de poder de sus aliados menores: MRN y MC.
El juego cociente natural demuestra que los jugadores de mayor peso en la izquierda (PRD) y en el centro (PRI) obtienen un pago mayor al obtenido en un juego no coalicional, sobre todo en el primero de ellos. Aquí se ve a importancia de encabezar una bancada. El caso de la derecha es un caso particular donde el juego coalicional le indica que es mejor ir solo.
En esta parte se abordan algunos casos hipotéticos de estructuras de coalición diferentes a la estructura natural B = {B C , B D , B I }. Se usan estructuras de coalición cuyo primer componente está relacionado con algunas coaliciones mínimas ganadoras del JMP original (coaliciones en W m ) más otros dos casos hipotéticos. Se presenta, en el cuadro 4, la comparación entre el ISS y los valores coalicionales.
Una primera observación a resaltar es que en las estructuras de coalición donde se ve involucrada una CMG (estructuras B 1, B 2 y B 5) los partidos que están dentro de ella reciben de forma equitativa un pago positivo con el VAD. Como antes, para fines de comparación, se usa el VCO como valor coalicional y al ISS como valor individual.
Conforme a lo establecido en el Cuadro 4, en la primera estructura de coalición B 1, propuesta para ver lo que sucede cuando los tres jugadores principales se unen, se tiene que, de acuerdo con el VCO, el PRI pierde poder y los que lo ganan son el PAN y el PRD, siendo este último el más beneficiado al aumentar su poder de decisión en más de un 15%, al grado de empatar en poder al PAN. Los demás jugadores grupales que no pertenecen a la CMG (a W m ) obtienen un poder nulo; esto último se cumple en los otros dos escenarios donde el primer componente de B j es una CMG, j = 2, 5.
En el segundo caso, con la estructura B 2, donde los dos principales partidos del centro hacen coalición con el principal partido de derecha, se beneficia al PRI y al PVEM con un 11% de poder más; por su parte, el PAN pierde poder de decisión. Se puede hablar entonces de una trampa del centro para aumentar su poder a costa de la pérdida del mismo de los demás partidos.
Por otra parte, con la estructura B 3 (donde los dos primeros lugares en peso atraen al último lugar) pasa algo peculiar. Se tiene que con esta estructura de coalición tanto el PRI como el PAN pierden poder, pero donde este último es el más perjudicado al volverse un jugador sin poder. Al jugador independiente de nada le sirve unirse a los dos más poderosos y sigue siendo nulo. Por otra parte, se puede ver que los demás partidos se ven beneficiados de esta estructura.
El cuarto escenario del Cuadro 4 muestra que con la estructura B 4, donde los dos principales partidos de izquierda se unen al partido en el poder, sucede algo similar al caso anterior. Ahora, el PRI nuevamente pierde poder, pero también pasa lo mismo con sus aliados de izquierda PRD y MRN, al grado de quitarles por completo su poder de decisión. Por el contrario, a excepción del PAN, los demás partidos aumentan su poder y el mayor compensado es el principal aliado natural del PRI, el PVEM, pues aumenta su poder en más de un 14%. En este caso, el PRI, en realidad se une a las izquierdas para quitarles poder y transferirlo a uno de sus aliados naturales.
Por último, con la estructura de coalición B 5 (CMG que contiene a partidos más pequeños) se obtiene que todos los partidos en la CMG aumentan su poder, el PRI obtiene un 60% del poder y los otros cuatro partidos un 10% cada uno. Con ello, los partidos más pequeños de esta coalición (MRN, MC y PES) son los más beneficiados al lograr empatar en poder al PRD.
Es así que se han presentado algunos casos posibles de un JC no natural de la LXIII CdD usando los distintos índices de poder. Sin duda, existe un sinfín de escenarios a discutir en este tipo de JC. En esta sección (y en la siguiente de la LXIV CdD) se muestran solo algunos de ellos, unos más probables de suceder que otros.
En este segundo caso de estudio se analiza la estabilidad política de la LXIV CdD, la cual comprenderá del año 2018 al año 2021; la forma en que se procede es de manera análoga a la que se siguió en el estudio anterior.
Después de las elecciones del 2018, la LXIV CdD quedó conformada como se muestra en el Cuadro 5.32
[i] Fuente: Elaboración propia con información del sitio http://www.diputados.gob.mx/.
Se puede ver que existe una gran reconfiguración de la LXIV Legislatura si se compara con la LXIII CdD. Ahora se tiene a MRN como primera fuerza y a sus aliados presidenciales,33 el PT y el PES, como cuarta y quinta fuerza, respectivamente. El PRI se encuentra ahora en un tercer lugar de peso y el PAN mantiene su segunda posición en el tablero, aunque de una manera mucho más débil si se compara con la Legislatura antes analizada. Con la llegada de MRN al juego político, el PRD (el mayor representante de la izquierda por mucho tiempo) se fue hasta las últimas posiciones.
Luego, si se toma en cuenta la cuota de mayoría q = 334 y los pesos del cuadro 5, el JMP para la LXIV Legislatura se puede escribir como:
Se encontró un total de 202 coaliciones ganadoras, un número grande comparado con la Legislatura anterior (152 para la LXIII CdD), ello debido a la distribución menos concentrada en las diferentes fuerzas políticas, excluyendo a MRN. Ahora el jugador 1, MRN, cuenta con veto.
Por otra parte, el conjunto de las 24 CMGs encontradas es:
Como se puede ver, el hecho de que haya más CMGs posibles para esta Legislatura se debe a que, a excepción de MRN, los demás partidos tienen un peso menos diferenciado entre ellos y donde las tres principales fuerzas políticas no concentran la gran parte de los diputados como en la otra Legislatura. Lo anterior propicia que existan CMGs de gran tamaño y que hasta el grupo independiente pueda ser necesario para ganar el JMP de forma mínima.
En el Cuadro 6, se hace una comparación del índice de Shapley-Shubik y del índice de Banzhaf de esta Legislatura.
Se observa que la repartición del poder se distribuye de manera concentrada en las dos primeras fuerzas donde MRN goza de un gran poder de decisión. El papel que antes tenía el PRI ahora lo tiene MRN, superando incluso el 60% de poder tomando en cuenta el valor de Shapley-Shubik. El poder del PRI ha disminuido considerablemente contando ahora con solo el 6% de poder de decisión. El PAN, a pesar de mantener su lugar como principal oposición, se ve disminuido en su poder (pasando de un 16 a un 12%). El PRD es el partido que se ha visto más perjudicado desde la llegada de MRN, al disminuir de manera considerable su poder (comparar con el Cuadro 2). Con el IB se tienen cifras parecidas.
Enseguida se abordan algunos escenarios del juego cociente y sus respectivos valores coalicionales. Al igual que en el primer caso de estudio se analizan algunas estructuras de coalición naturales y no naturales.
Tomando como punto de partida un escenario hipotético donde se respete la ideología de partidos en la LXIV CdD, se tendría la siguiente partición natural B = {B I , B D , B C }, donde B I = {MRN, PT, PRD, MC } es el bloque de la izquierda, B D = {PAN, PES} es el bloque de la derecha y B C = {PRI, PVEM, IND} es el bloque del centro. Al igual que en la Legislatura anterior, se supone que el jugador IND está dentro del centro.
Luego, con la partición antes presentada y con el enumerado correspondiente de cada partido siguiendo el Cuadro 5, el conjunto B del juego cociente sería:
Tomando en cuenta la cuota q = 334 y el peso de cada partido (véase el Cuadro 5) se tendría que:
Con las consideraciones antes hechas, se presentan, en el Cuadro 7, los valores de Shapley-Shubik originales de cada jugador y los valores coalicionales de Aumann-Dreze y de Owen.
Se puede ver que el VAD es nulo para todos los partidos pues ninguna coalición rebasa la cuota de mayoría; el análisis coalicional se hace con el VCO.
El Cuadro 7 muestra lo que hubiese podido ser (y que podría suceder) si los partidos juegan en coaliciones de forma natural. En general, se observa que, a diferencia de la Legislatura anterior, todos los partidos principales de cada bancada pierden poder de decisión con el VCO, donde, en algunos casos, el poder es captado por algunos de sus aliados.
Con este juego natural, la bancada de la izquierda es la que se vería más perjudicada en el juego cociente, pues en conjunto perderían más de un 8% de poder si se compara con el ISS del juego original. MRN baja en más de un 3% su poder, el PT, MC y el PRD igualarían en su VCO a poco más de un 1% de poder, lo cual significa una pérdida de poder político con respecto al JMP original.
Por otro lado, el centro es el más beneficiado en el juego coalicional aumentando su poder en poco más de 7%, pese a que su principal representante, el PRI, pierde poder de decisión; sin embargo, sus aliados superan dicha pérdida de acuerdo con el VCO.
Un escenario intermedio pasaría con la derecha ya que en conjunto mantendrían casi el mismo poder, donde el PAN le transfiere poder a su aliado (al PES).
Para esta parte del análisis se consideran algunos casos hipotéticos de estructuras de coalición diferentes a la estructura natural. Así, al tomar en cuenta algunas coaliciones de W m más otros casos hipotéticos, se presenta, en el Cuadro 8, la comparación entre el ISS y los valores coalicionales.
En primer lugar, se observa que en las estructuras de coalición que contienen una CMG (todas excepto B1) los partidos, al formar parte de ella, reciben un pago positivo con el VAD. Un caso peculiar es el obtenido con la estructura B3 donde se pone de manifiesto la eficiencia relativa del VAD y donde el pago de los jugadores en la segunda coalición de tal estructura es no equitativo; esto último sí pasa en los demás casos donde el VAD es no nulo. Sin embargo, para fines de comparación se usa el VCO como valor coalicional y al ISS como valor individual.
En general, se observa que con el VCO los partidos dentro de la CMG reciben una transferencia de poder de forma equitativa por parte de MRN. En todos los escenarios MRN no se ve beneficiado con el VCO; esto no pasaba con el PRI en la Legislatura anterior.
En la primera estructura de coalición, B1, se analiza la coalición presidencial encabezada por MRN. Dado que tal coalición no pertenece al conjunto de las CMGs (de hecho, ni a las CGs), todos los partidos reciben un valor positivo del VCO excepto sus propios aliados. Así, los que más se benefician en este caso son los partidos pequeños.
No obstante, si a la coalición presidencial de MRN y aliados se le une MC, dicha coalición ya forma parte de las CMGs. A pesar de que MRN pierde un 3% de poder, a sus demás aliados les aumenta de forma equitativa hasta un 12.5% de poder de decisión siguiendo el VCO.
Al tomar en cuenta la estructura mínima en votos del conjunto de las CMGs del JMP original (a B3) se observa que el poder es repartido totalmente entre MRN (con un 75%) y el PAN (con un 25%). En realidad, este escenario es poco probable de suceder dadas las diferencias tanto ideológicas como políticas de estos dos partidos.
Si se toma en cuenta la CMG dentro de B4, donde MRN junto con sus aliados presidenciales hacen coalición con el PRI, pasa algo similar al segundo caso donde el papel de MC lo desempeña ahora el PRI.
Por último, se presenta un escenario alternativo para ganar por parte de MRN, sin la necesidad de contar con sus aliados presidenciales. Lo anterior se representa en la estructura B5 donde MRN se alía con el centro y con el PRD, la cual representa una de las CMGs más grandes. En este caso el poder de MRN se ve mermado en un 6% pero se compensa con un 10% de poder en cada uno de sus nuevos aliados.
Finalmente, para fines comparativos entre los principales partidos políticos de las Legislaturas analizadas, se presentan, en el Cuadro 9, algunos datos ya mostrados, con la inclusión de algunos promedios en los valores coalicionales de los juegos no naturales. Para el análisis, se utiliza el ISS como valor individual y el VCO como valor coalicional.
De este último cuadro se concluye que el PRI se ve favorecido más con los valores coalicionales en ambas Legislaturas, en particular con los juegos no naturales, contrariamente a lo que sucede con el PAN y MRN quienes ven disminuido su poder de decisión al asociarse con otros partidos. Por su parte, el PRD aumenta su poder con los juegos naturales en la LXIII CdD y con los juegos no naturales en la LXIV CdD.
Al comparar los datos por Legislaturas, saltan a la vista los grandes cambios en el poder político de cada partido, donde MRN ha sido el gran ganador y los otros partidos los perdedores. En comparación con el poder del PRI en la LXIII CdD, MRN tiene incluso más poder de decisión en la presente Legislatura, donde de manera individual ha pasado de tan solo un 4.3% a un 66% de poder; donde un poder mínimo de 2.8% en su bancada de izquierda se ha transformado en un 62.5% del mismo; y, finalmente, donde su relación con otros partidos fuera de su ideología ha pasado de un 4.3% a un 62% de poder en promedio con los casos ya analizados.
Esta investigación permitió analizar el poder de decisión de los partidos políticos en las Legislaturas LXIII y LXIV, considerando como variables los índices de valor de decisión para cada partido (individuales) y para cada coalición (coalicionales) a partir de códigos de simulación de juegos cooperativos en Scilab, fundamentados en la teoría de juegos.
La importancia de cuantificar el poder político radica en una mejor lectura de cada uno de los partidos. Se ha encontrado así, con ayuda de los valores individuales, que se ha reconfigurado por completo la Cámara de Diputados, donde, en tan solo tres años, MORENA ha aumentado en más de un 60% su poder de decisión y el PRI lo ha perdido en casi un 50%. Por su parte, el PAN y el PRD han visto disminuido su poder, aunque de manera menos marcada, donde este último partido prácticamente ya no es imprescindible en las decisiones políticas.
Por otra parte, formar coaliciones con otros partidos puede ser benéfico para unos y perjudicial para otros, ello en el sentido de que algunos ganan y otros pierden poder de decisión con respecto a su valor individual. Así, se pudo verificar que el PRI es el partido más beneficiado en ambas Cámaras al hacer coaliciones, en ambas formas de realizar las coaliciones: natural y no natural; MRN mantiene su poder o incluso lo disminuye haciendo coaliciones; el PAN siempre se ve perjudicado en su valor coalicional; por último, el PRD gana poder al menos con alguno de los juegos coalicionales (con los partidos de izquierda en el caso de la LXIII CdD y con las coaliciones PAN+PRI+MC+PVEM+IND y MRN+PRI+PRD+ PVEM+IND en el caso de la LXIV CdD).
Aunque algunos partidos pierdan poder dentro de su coalición, no se debe perder de vista que muchas veces ese poder es transferido a los miembros de su bancada, lo cual puede contribuir al fin último, que es la mayoría calificada en cada caso, para aprobar los acuerdos. Lo anterior con las suposiciones de que exista cohesión y disciplina de cada partido a lo largo de una Legislatura y que la transferencia de poder se pueda hacer entre cualquier partido, incluyendo aquellos partidos que son minorías. La manera en que los partidos decidan formar parte de alguna coalición dependerá de los beneficios y costos que cada uno de ellos prevea, así como de otras variables externas al juego como lo es el “influyentismo” definido por Nacif (2003) y retomado en trabajos como el de Larios Ferrer (2022).
Las ganancias y pérdidas de capacidad decisoria encontradas en los diferentes juegos de las Cámaras abordadas son consecuencia de la interacción entre las diferentes fuerzas políticas, lo cual conlleva a un buen número de escenarios cooperativos para poder aprobar determinadas propuestas. Queda como agenda futura de investigación realizar este tipo de estudios para legislaturas subsecuentes y para otros parlamentos como la Cámara de Senadores. Además, se puede seguir trabajando con la dinámica de los juegos repetidos y ver los casos donde se mantiene la estabilidad dada por estos índices de poder discutidos. Por último, se puede abundar más en la variable de estructura de incentivos y su relación con el tipo de asuntos a decidir en las Legislaturas.
Se puede decir que hace falta realizar este tipo de análisis interdisciplinario que permita estudiar la conducta política dentro de los Congresos mexicanos. A los partidos y a sus agentes involucrados puede servir de mucho para así lograr aprobar sus propuestas.
Carreras, F. 1992. Estudio coalicional de los parlamentos autonómicos españoles de régimen común. Documento de Trabajo 92-13 (Serie de Economía 08): 1-21.
F. Carreras 1992Estudio coalicional de los parlamentos autonómicos españoles de régimen comúnDocumento de Trabajo 92-13 (Serie de Economía 08)121
Larios Ferrer, J. L. 2022. Estabilidad e inestabilidad políticas en las LXII y LXIV Legislaturas mexicanas, desde la perspectiva de la teoría de juegos. Revista Mexicana de Ciencias Políticas y Sociales, 67(244). https://doi.org/10.22201/fcpys.2448492xe.2022.244.72754.
J. L. Larios Ferrer 2022Estabilidad e inestabilidad políticas en las LXII y LXIV Legislaturas mexicanas, desde la perspectiva de la teoría de juegosRevista Mexicana de Ciencias Políticas y Sociales6724410.22201/fcpys.2448492xe.2022.244.72754
Owen, G. 1977. Values of games with a priori unions. En R. Henn y O. Moeschlin (eds.), Mathematical economics and game theory. Nueva York: Springer Verlag, 76-88.
G. Owen 1977Values of games with a priori unions R. Henn O. Moeschlin Mathematical economics and game theoryNueva YorkSpringer Verlag7688
Owen, G. 1981. Modification of the Banzhaf-Coleman index for games with a priori unions. En M. J. Holler (ed.), Power voting and voting power. Wurzburg, Alemania: Physica-Verlag, 232-238.
G. Owen 1981Modification of the Banzhaf-Coleman index for games with a priori unions M. J. Holler Power voting and voting powerWurzburg, AlemaniaPhysica-Verlag232238
Shapley, L. S. 1963. Some topics in two-person games. En Dresher, M., Shapley, L. S. y Tucker, A. W. (eds.), Advances in game theory. Princeton: Princeton University Press, 1-28. https://doi.org/10.1515/9781400882014-002.
L. S. Shapley 1963Some topics in two-person games M. Dresher L. S. Shapley A. W. Tucker Advances in game theoryPrincetonPrinceton University Press12810.1515/9781400882014-002
Vargas Hernández, J. G. 2006. La nueva economía política en la transformación institucional del Estado-Nación. Problemas del Desarrollo. Revista Latinoamericana de Economía, 37(145): 31-51.
J. G. Vargas Hernández 2006La nueva economía política en la transformación institucional del Estado-NaciónProblemas del Desarrollo. Revista Latinoamericana de Economía371453151
[12] Este acontecimiento sucedió durante las elecciones del 20 de diciembre de 2015 en España, siendo este un fenómeno político trascendente para ese país, pues ninguna de las fuerzas políticas logró obtener la mayoría en el Congreso. Lo anterior llevó a que, durante más de un año, la negociación entre los diferentes partidos para poder formar una coalición ganadora fuera infructuosa. Después del 20D, y durante el periodo de incapacidad para formar gobierno, se tuvieron algunas repercusiones económico-financieras inmediatas como lo fue el bajo desempeño del Ibex 35, su principal indicador financiero, y el efecto negativo sobre su prima de riesgo país.
[13] Para el caso de México, la aprobación de la reforma energética, el 12 de diciembre de 2013, fue el tema más trascendente en el ámbito económico de los últimos 20 años (cabe recordar que el Tratado de Libre Comercio de América del Norte se firmó en 1992).
[14] Muchos de los autores de la NEP pertenecen también a la teoría de elección pública, la cual usa la teoría económica para estudiar problemas típicos de ciencias políticas. Dentro de las ciencias políticas, es considerada parte de la elección pública positiva, la cual estudia las decisiones colectivas o públicas de los agentes políticos. Sus líneas de investigación se han diversificado en diferentes ámbitos de la ciencia política y de la economía, destacándose, sobre todo, en temas electorales y de votaciones (López Sandoval 2016). La NEP tiene como principal presupuesto que se converge a la eliminación o relativización del supuesto de que los actores políticos actúan motivados por el bien común, al tiempo que los concibe motivados por una decisión racional (rational choice) permitiéndoles obtener el máximo beneficio personal (Vargas Hernández 2006).
[15] La TEV tuvo sus antecedentes con el trabajo de Hotelling (1929), donde se desarrolló un modelo espacial de competencia entre empresas. El primer trabajo en transformar las ideas espaciales de Hotelling en modelos formales de competencia política fue el de Downs (1957). Algunos de los avances recientes dentro de la TEV se preocupan por seguir describiendo a los agentes políticos, por una parte, cuando estos son los electores (véanse, por ejemplo, los trabajos de Hinich y Munger (1994) y el de Bonilla (2004)) y, por otra, donde estos agentes son los partidos o coaliciones de los mismos. Para fines de esta investigación, la conducta del electorado se deja de lado, pero se toma en cuenta, implícitamente, como aquel que define las condiciones iniciales de los diferentes juegos abordados. EL presente trabajo se enfoca en los partidos y sus coaliciones como los agentes a estudiar.
[16] Desde esta perspectiva teórica en que se fundamenta el análisis del trabajo, se hace abstracción de problemas relativos a los factores exógenos que inciden en la toma de decisiones en los Congresos, y que circunscriben al cálculo racional y estratégico de legisladores y partidos políticos para decidir y ver si adoptan o no una estrategia cooperativa en la toma de decisiones en esa institución.
[17] Un juego cooperativo es aquel donde algunos jugadores hacen equipo mediante un acuerdo vinculante y reciben una recompensa en forma de pago, la cual dependerá de las reglas del juego y de la situación de cada jugador. Por otro lado, en un juego no cooperativo no es plausible la cooperación entre jugadores y en su lugar actúan de manera racional buscando la mejor estrategia que los lleve a obtener un máximo pago, tomando en cuenta las estrategias de los demás jugadores.
[18] El núcleo de un juego es el conjunto que contiene las asignaciones factibles para cada jugador, y las cuales no pueden mejorar.
[19] En el presente trabajo, no se toma en cuenta este tipo de soluciones, pues muchas veces este conjunto es vacío.
[20] Dichos valores otorgan información del jugador en cuanto a su importancia de participación en el juego. Entre más grandes sean estos valores, mayor relevancia tendrá el jugador para ganar el juego.
[21] Por lo pronto, entiéndase partición como sinónimo de división de un conjunto; más adelante en el trabajo, se define de manera formal este concepto.
[22] Es decir, distintas particiones del conjunto total de jugadores; entre más grande sea este conjunto, más estructuras de coalición se podrán formar.
[23] Por el momento, piénsese en un juego cociente como aquel que toma en cuenta a ciertos jugadores representantes de su coalición y donde se toma a las coaliciones como jugadores grupales, además de tomar en cuenta a los jugadores individuales dentro de sus coaliciones; en el trabajo se define de manera formal este tipo de juego.
[24] Scilab es un software para análisis numérico, con un lenguaje de programación de alto nivel para cálculo científico. Se usa este software por su analogía con MATrix LABoratory (Matlab) pero de uso libre y por ser apto para dar solución a este tipo de problemas.
[25] Estabilidad en el sentido de que con el IS se obtiene la valoración de la unión de cada jugador dentro de las coaliciones, de las cuales no forma parte de ellas en un principio.
[26] Coaliciones dentro del conjunto de jugadores N tales que tienen un valor unitario para el caso de un JS. En general, se trata de aquella coalición donde se gana el juego, aunque se podría prescindir de algunos jugadores para que ello suceda.
[27] Se trata de aquellas coaliciones ganadoras donde todos los jugadores son necesarios para ganar el juego.
[28] Los siguientes conjuntos son conjuntos de índices: I = {1, 2, …, n}, I = {1, 2, …, ∞} e I = [0, 1].
[32] Véase, por ejemplo, el trabajo de Aumann-Dreze (1974).
[33] Una notación más general sería definir a M ≡ {n1, n2, ..., nm}, con nj representante de la subcoalición Nj.
[34] Entiéndase por subcoalición como un grupo de jugadores de una determinada coalición, la cual puede ser desde un jugador perteneciente a dicha coalición hasta la coalición entera.
[35] Se hacen estas aclaraciones puesto que en la literatura consultada no se hace énfasis a la hora de poner en práctica dicho valor; en todos los casos solo se muestra el resultado; en algunos casos sí se muestra el procedimiento, pero no de la forma en que aquí se presenta.
[36] Se aclara que, en esta clase de índices, se parte de la perspectiva teórica de elección racional y, por tanto, se presupone que, para los escenarios simulados, los legisladores que integran cada partido se comporten con disciplina para votar en el mismo sentido, es decir, que exista un alineamiento partidista y no se prejuzgue el asunto de que se trate la decisión en juego, aunque en los hechos sea una práctica común en el ámbito de los congresos. Un modelo donde exista la no alineación puede consultarse en Larios Ferrer (2022).
[37] Cabe mencionar que en este tipo de juegos racionales se dejan fuera ciertas externalidades (variables relativas a la disciplina, unidad y coherencia al interior de cada partido o coalición) que pudieran cambiar la manera de votar de los diputados. Los costes de tener elecciones racionales podrían ir en varios sentidos, desde el desprestigio de los diputados por votar a favor o en contra de ciertos acuerdos, hasta la no relección o elección en otros cargos por ese tipo de decisiones. A su vez, los diputados pueden tener ciertos beneficios por su disciplina dentro de su bancada como lo es el respaldo de la misma ante iniciativas propias de los diputados y de promoverlos a otros cargos de función pública. De igual manera, puede haber otro tipo de incentivos o desincentivos para los diputados, partidos o coaliciones que vengan de agentes internos o externos a las Cámaras; ello, dependiendo de los grupos de interés, de que se aprueben o no ciertas iniciativas. Para ver los efectos de indisciplina dentro de las bancadas, lo cual se traduce en cierto nivel de “traición política”, se puede consultar el trabajo de Larios Ferrer (2022).
[38] La ciencia matemática es necesaria para abordar la parte de fundamentos matemáticos como conceptos y teoremas que sustentan cada uno de los juegos e índices discutidos; además, se agregaría la parte de lógica matemática, para programar los diferentes códigos en Scilab. De la ciencia económica se abstrae el enfoque de economía positiva, en específico de la teoría de juegos cooperativos. Por último, de la ciencia política se retoman los pensamientos de algunos autores que siguen la tipología del espectro izquierda, centro y derecha (Bobbio (1996), como se citó en Heywood (2017), y el análisis de las diferentes votaciones que se dieron en las Cámaras estudiadas.
[39] Se aclara que el poder de decisión en estos casos de estudio está relacionado con el número de votos de cada partido y coalición, el cual puede variar de acuerdo con los movimientos que surjan en las Cámaras. Por ejemplo, cambios de adscripción partidista entre legisladores y legisladoras, las licencias para separarse del cargo y los relevos en comisiones legislativas pueden cambiar dicho poder de decisión a lo largo de la Legislatura. Para fines del estudio de los casos, se supone que esta composición se mantiene fija, despreciando aquellos cambios como los mencionados anteriormente.
[40] Se toma la parte entera redondeada hacia arriba. Dicha cuota coincide con lo que se menciona en el Sistema de Información Legislativa (SIL): “...Considerando que la Cámara de Diputados está integrada por 500 legisladores, se requieren 334 votos para alcanzar una mayoría calificada —o un número menor, según el total de asistentes a la sesión”. Información en línea: http://sil.gobernacion.gob.mx/Glosario/definicionpop.php?ID=152.
[41] En el caso de las Legislaturas mexicanas, se han vislumbrado tres ideologías: izquierda, centro y derecha. Cuando las coaliciones son formadas por partidos de una misma ideología, se entiende que es una coalición natural; en caso contrario, se referirá a tal coalición como no natural.
[42] Para fines de comparación, se decide usar en adelante el valor de Shapley-Shubik y no el valor de Banzhaf, pues se considera que el primero de ellos representa mejor el poder de decisión de los partidos políticos, al tratarse de un grupo homogéneo y donde cada uno de sus miembros adopta una misma forma de voto.