Introducción
La competitividad generada por la globalización obliga a las organizaciones con fines
de lucro a buscar mecanismos y estrategias que les mantengan en la participación del
mercado. Indicadores como la producción y los costos se vinculan y pueden asociarse
con un indicador único, la productividad, entendida como el cociente de lo producido
y los requerimientos. En este sentido, el objetivo primordial para los directivos
de las organizaciones es la minimización de los costos de producción. Para minimizar
costos, existen diferentes estrategias, una de ellas se basa en el balanceo de las
líneas de producción. Las líneas de ensamble han sido utilizadas tradicionalmente
para producir grandes cantidades de un modelo único. Este modelo es denominado línea
de ensamble de un solo modelo. Por otra parte, existen los modelos de líneas de ensamble
de modelo mixto, en el cual el sistema de ensamble es lo suficientemente flexible
para producir más de un modelo de manera mezclada y sin patrones o tendencias; la
tercera clasificación es conocida como línea de ensamble de modelos múltiples, caracterizada
por producir distintos tipos de productos de una familia en una misma línea, requiriendo
una configuración previa al cambio de producción (Kumar y Mahto 2013, 30), sin embargo, su balanceo requiere técnicas diferentes de las tradicionales (Murillo-García et al. 2018, 1).
Por otra parte, las líneas de ensamble pueden clasificarse de acuerdo con las restricciones
del número de trabajadores por estación de trabajo: las líneas de ensamble simples,
en las que por las dimensiones del producto solo es posible asignar un trabajador
por estación; líneas de ensamble a dos lados, son denominadas así por presentar la
factibilidad de asignar uno o dos trabajadores a cada estación de trabajo. Finalmente,
las líneas de ensamble multi-tripuladas (MAL), que se caracterizan por asignar uno,
dos, tres o más trabajadores por estación de trabajo (Zamzam y Elakkad 2021, 734) como se muestra en la Figura 1.
Figura 1
Tipos de líneas de ensamble de acuerdo con el número de trabajadores por estación.
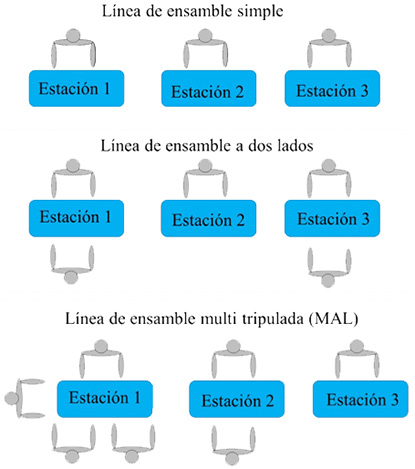
Fuente: Elaboración propia del modelo de Zamzam y Elakkad (2021, 734)
Una de las formas de línea de ensamble más común es conocida como multi-tripulada.
Sin embargo, no ha sido explorada en su totalidad a pesar de ser común en los procesos
de producción. Lo anterior genera problemas de optimización de estaciones de trabajo
en líneas de ensamble; tienen sus orígenes en Talbot y Patterson (1984, 86) quienes describen un algoritmo de programación entera para asignar tareas, y determinando
el mínimo número de estaciones de trabajo para balancear las estaciones. Concluyen
que el algoritmo puede encontrar resultados óptimos en un tiempo computacional razonable
para líneas de ensamble con máximo de 50 tareas. Adicionalmente, se han realizado
propuestas para resolver el MAL bajo un enfoque flexible denominado FMAL (Cantos, Vidal, Sato y Magatao 2019, 1). Mediante un modelo de programación lineal entero mixto, basado en un procedimiento
heurístico. Estudios adicionales consideran las habilidades de los trabajadores como
factor de interés en el balanceo de líneas de ensamble (Esfandyari y Roshani 2020, 66). Por otra parte, se estudia la forma de la línea de ensamble con forma de U (Zakaraia, Zaher y Ragaa 2021, 278). Esta es también una línea de ensamble multi-tripulada.
El ALBP (the assembly line balancing problem) o, en español, problema de balanceo de línea de ensamble) es conocido como un problema
NP-hard lo cual implica distribuir las tareas necesarias para fabricar cualquiera de los
productos a ensamblar entre las estaciones de trabajo a lo largo de la línea de fabricación
(Grzechca y Foulds 2015, 2002). Por otra parte, existen variaciones del problema de ensamble tales como SALBP
(simple assembly line balancing problem), SALBP-1, SALBP-2 y SALBP-F (Peña-Orozco y Jiménez-Gómez 2019, 178). Algunos métodos utilizados en la solución de este tipo de problemas se centran
en los heurísticos como el GRASP (greedy randomize adaptive search procedure) (Moreno-Ramírez 2018, 28), incluso este heurístico se utilizó en combinación con un software en lenguaje de programación Visual Studio 2013 Community y MS Access, para almacenar
información. Se calculó el tiempo estándar en cada una de las estaciones de trabajo,
para, posteriormente, balancear la línea de ensamble. Los resultados de esta investigación
impactan en la reducción del tiempo ocioso en la línea de ensamble en un 84.89%. Además,
se logró disminuir de 6 a 4 el número de estaciones de trabajo, logrando 33.33% de
ahorro anual en dinero. También se aumentó la eficiencia de la línea de 35.24% a 72.24%
(González et al. 2017, 1). Adicionalmente se han utilizado algoritmos heurísticos como el GRASP para abordar
este problema (Paredes-Quevedo et al. 2022, 50).
El problema de optimización de líneas de ensamble multi-tripuladas tiene sus orígenes
en la línea de ensamble de un solo modelo (Kumar y Mahto 2013, 42) propuesto por Talbot y Patterson (1984, 86) y resuelto mediante un algoritmo de programación entera. Los resultados reportan
el número óptimo de estaciones de trabajo en diferentes instancias de un máximo de
111 tareas; sin embargo, el costo computacional es elevado al ser considerado también
como un problema NP. El problema de líneas de ensamble multi-tripuladas es afectado
por diferentes factores: el número de trabajadores en cada estación de trabajo desarrollando
modelos matemáticos que lo representen con la intención de minimizar el número de
trabajadores y, en una segunda instancia, minimizar el número de estaciones de trabajo
mediante programación lineal (Yazdanparast y Hajihosseini 2011, 842). A pesar de propuestas de métodos exactos de programación lineal mejorados (Sato-Michels, Cantos-Lopes y Magatão 2020, 1), la complejidad computacional es una limitante en la búsqueda exhaustiva, por lo
que cual se han explorado enfoques basados en heurísticos como la optimización de
colonia de hormigas (Roshani y Roshani 2012, 614), en la búsqueda de minimizar el tiempo de ciclo.
Debido a que los tiempos de las tareas dependen de la concentración de trabajadores
en la estación, se presentó una formulación matemática para resolver este problema
con el objetivo de minimizar el número de estaciones (Sepahi y Jalali-Naini 2014, 68); se desarrollaron cuatro procedimientos heurísticos para resolver este problema.
Adicionalmente, el problema fue resuelto mediante el algoritmo de búsqueda tabú (Roshani y Giglio 2020, 194) utilizando dos mecanismos de generación de vecindarios, denominados intercambio
y mutación, colaborando uno con otro de manera efectiva para encontrar nuevas soluciones
factibles mediante dos listas tabú.
Por otra parte, el problema de balanceo de líneas para estaciones de trabajo multi-tripuladas
fue abordado mediante algoritmos genéticos (Jithendrababu, RenjuKurian y Pradeepmon 2013, 778); demostrando mejorar la eficiencia de la línea de ensamble comparado con el sistema
existente. Adicionalmente, se ha utilizado el enfoque de recocido simulado en la búsqueda
por hacer más eficientes los resultados del problema (Roshani y Ghazi 2017, 34).
Otra propuesta de solución del problema de balanceo de líneas de ensamble multi-tripuladas
se basa en el uso de algoritmos genéticos (Zamzam, Sadek et al. 2015, 59). Se propuso un nuevo indicador para evaluar el número máximo de trabajadores en
la estación de trabajo, alcanzando valores óptimos en 60 instancias de 62 con mejoras
en los resultados del 25% al 50%.
Al problema de balanceo de líneas de ensamble multi-tripuladas le fue adicionado un
nuevo problema, el de los espacios; de tal manera que se busca minimizar el número
de trabajadores en cada estación de trabajo, el número de estaciones de trabajo y
el espacio o área de trabajo. Se utilizaron algoritmos genéticos (Zamzam y Elakkad 2021, 738). El MAL se ha resuelto considerando la posibilidad de que varios trabajadores realicen
simultáneamente distintas tareas en un mismo puesto de trabajo. En la mayoría de los
casos, se supone que los tiempos de las tareas son deterministas; toman en cuenta
las posibles interferencias entre trabajadores y trata el MALBP con tiempos de trabajo
en función del número de trabajadores en la estación. Se desarrollan diferentes procedimientos:
resoluciones con base en un modelo matemático, dos procedimientos relax-and-fix, una heurística basada en la resolución de un problema de partición con restricciones
(denominada “HEUR_PART”) y un conjunto de otras variantes del procedimiento HEUR_PART.
Los experimentos computacionales indican que HEUR_PART y la variante HEUR_PART_SGL
son las propuestas que mejor funcionan (Andreu-Casas, García-Villoria, Pastor 2021,
96). El MAL se ha utilizado también para resolver problemas de manera análoga a los
problemas de optimización del campo electromagnético. En todos los casos considerándose
un problema de alta complejidad computacional (Şahin y Kellegöz 2018, 6487).
Por lo anterior, en el presente trabajo se buscar solucionar el problema de balanceo
de líneas de ensamble para estaciones de trabajo multi-tripuladas; minimizando el
número de trabajadores y el número de estaciones de trabajos mediante un algoritmo
genético. Comparando los resultados con los presentados en la literatura.
Presentación de la problemática
El problema de balanceo de líneas de ensamble multi-tripuladas (MALB) consiste en
asignar un conjunto de tareas a un grupo de trabajadores de manera organizada y dividida
mediante estaciones de trabajo, minimizando el número de estaciones de trabajo y el
número de trabajadores en cada estación de trabajo. De manera formal, el modelo puede
ser representado como uno de programación lineal con dos funciones objetivo:
La ecuación (1) busca minimizar el número de estaciones de trabajo en la línea de
ensamble; la ecuación (2) es la función objetivo que busca minimizar el número de
trabajadores de manera que el problema es considerado bi-objetivo.
Adicionalmente, el modelo de programación lineal tiene un conjunto de restricciones
para cada una de las funciones objetivo por lo que a continuación se describen:
Función objetivo: FF (1) = min (Ns) … (1)
Sujeta a las restricciones:
Función objetivo: FF (2) = min (Nm) … (2) Sujeta a las restricciones:
La restricción (3) asegura que la suma de los tiempos de tareas asignadas a una estación
en particular no exceda el tiempo de ciclo. La restricción (4) asegura que se respete
la precedencia de las actividades. La restricción (5) asegura que cada tarea i es asignada solo a un trabajador y a una estación. La ecuación (6) es una restricción
que asegura la precedencia de las actividades al asignarlas a los trabajadores.
Método de solución
Descripción general del AG
Para resolver el MALB se propone aplicar un algoritmo genético el cual primero generará
un número n de soluciones aleatorias.
Cada solución será evaluada en la función costo la cual depende del número de estaciones,
el número de trabajadores y los tiempos muertos. Una vez que cada solución es evaluada,
se hará una selección de una población refinada por medio de elitismo y torneo.
Sobre la población evaluada, a cada solución se le aplicará un cruce dependiente de
la posición de trabajos (JBX), el cual funciona de manera natural para problemas de
secuenciación de tareas donde el orden de operaciones es crucial, pero, hasta nuestro
conocimiento, no se ha aplicado todavía para este problema. Una vez realizado el cruce,
se aplica una mutación en dos puntos con cierta probabilidad.
Otra parte original de este trabajo es la especificación de la función costo, la cual
pondera el número de estaciones de trabajo, el número de trabajadores asignados y
castiga soluciones con tiempos muertos altos, en lugar de aplicar un rebalanceo para
evitar estos tiempos.
Esto hace que el AG propuesto sea más sencillo de implementar y que realmente se vea
la fortaleza del proceso en descartar de manera iterativa soluciones con tiempos muertos
indeseables en lugar de implementar un proceso dedicado a esta situación como se ha
realizado en trabajos anteriores.
Codificación y decodificación de solución
Para una instancia del MALB con n trabajos por procesar, la codificación de cada solución del AG será una permutación
de los n trabajos. Para decodificar cada solución, la cadena de n trabajos se leerá de izquierda a derecha, y el orden en que aparezcan los trabajos
será el orden en que son procesados por el sistema. La Figura 2 muestra un ejemplo de cómo una codificación de 5 trabajos se procesa en una línea
multi-tripulada de 3 estaciones.
Figura 2
Ejemplo de codificación y decodificación de una secuencia de 5 trabajos.
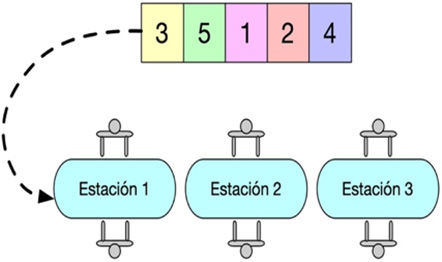
Fuente: Elaboración propia.
Por supuesto, se puede dar el caso en que un trabajo no pueda realizarse al no haberse
cumplido las restricciones de precedencia; es decir, los trabajos precedentes del
trabajo a realizar no se han procesado aún. Para este caso, se toma una pila de trabajos
que no se han podido procesar, cuando ya se han tomado todos los trabajos de la solución,
se revisa si la pila está vacía o no. En caso de tener trabajos pendientes, estos
se van procesando con la política de primera entrada, primera salida. Si el trabajo
seleccionado ya se puede procesar, se saca de la pila, en caso contrario, se toma
el siguiente trabajo de la pila.
Esto se repite hasta que la pila quede vacía, con esto se asegura cumplir la precedencia
de trabajos y que todos ellos sean considerados para especificar el número de estaciones,
el número de trabajadores y evaluar los tiempos muertos implicados en cada solución.
Función costo y tratar tiempo muerto como castigo
Cada solución del AG será evaluada conforme al número de estaciones de trabajo N
s
, al número de trabajadores N
t
y al número de N
m
de trabajadores que sobrepasen el umbral de tiempo muerto definido por el usuario.
Así, para una solución s
i
, la función costo a minimizar por el AG está definida como:
Donde cada α
i
es un peso que pondera cada objetivo de la función para favorecer o igualar la importancia
de cada uno de ellos. Un punto relevante del trabajo es trabajar el número de trabajadores
con tiempos muertos altos en la función costo, esto simplifica el cómputo de las estaciones
de trabajo y trabajadores que implica cada solución y deja el rebalanceo de la línea
al AG, a diferencia de trabajos anteriores.
Selección, elitismo y torneo
Para la parte de selección, se utiliza primero elitismo; se toman las dos mejores
soluciones (las que tenga un menor costo) como parte de la población refinada. Después,
el resto de n - 2 soluciones en la población se selecciona por medio de torneo. De la población
original se eligen dos soluciones de manera aleatoria y se selecciona la que tenga
un menor valor en la función costo; este proceso se repite n - 2 veces para tener una población refinada completa.
Cruce JBX
El operador de cruce utilizado en el AG es el cruce basado en trabajos (JBX). En este
cruce se definen dos subconjuntos aleatorios J
A
y J
B
tales que J
A
∪ J
B
= J y J
A
∩ J
B
= ∅. Para dos secuencias de trabajos OS
1 y OS
2, se van a obtener dos nuevas secuencias OS ’1 y OS ’2 donde las operaciones de los trabajos J
A
se colocan en OS ’1 en el mismo orden en que aparecen en OS
1, y las operaciones de los trabajos J
B
se ponen en las posiciones vacías de OS ’1 guardando el orden de izquierda a derecha en que aparecen en OS
2. Se obtiene otra solución OS ’2 tomando primero las operaciones de J
B
en las mismas posiciones de OS
2 y llenando los espacios vacíos de OS ’2 con las operaciones de J
A
en OS
1 en el orden en que aparecen. La Figura 3 presenta un ejemplo del cruce JBX para dos soluciones, cada una de 5 trabajos.
Figura 3
Ejemplo de cruce JBX para soluciones de un problema con 5 trabajos.
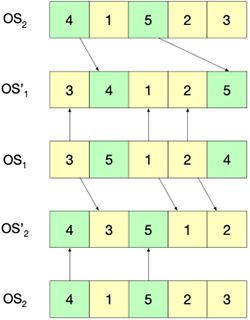
Fuente: Elaboración propia.
Mutación
La mutación de cada solución se hace con cierta probabilidad por intercambio, en donde
se seleccionan dos posiciones aleatorias de la solución seleccionada y se intercambian
sus elementos para obtener una nueva solución. La Figura 4 muestra un ejemplo de la mutación para una solución con 5 trabajos.
Figura 4
Ejemplo de mutación por intercambio.
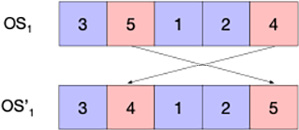
Fuente: Elaboración propia.
El diagrama de flujo del AG se presenta en la Figura 5.
Figura 5
Diagrama de flujo del AG.
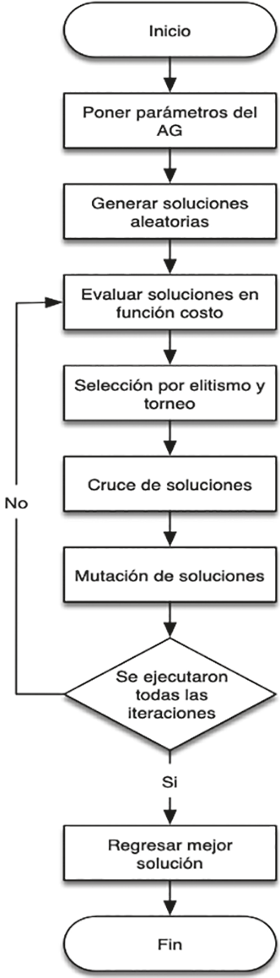
Fuente: Elaboración propia.
Características del código y máquina de prueba
El AG se implementó en Matlab R2015a (TM) en una máquina Intel Xeon W a 2.3 GHz y
128 GB de RAM. El código fuente está disponible en Github (https://github.com/juanseck/GAMmALB). Para probar la efectividad del AG se tomaron cuatro problemas con diferentes tiempos
de ciclo del banco de prueba presentado en CITA.
Descripción de indicadores y pruebas estadísticas
Para comparar el rendimiento del algoritmo propuesto contra los otros métodos de solución,
se tomará en cuenta el número de trabajadores (NW) y el número de estaciones de trabajo
(NS) que alcance cada método en cada instancia de prueba.
Mientras menores sean estos indicadores, mejor será la solución calculada.
Para el algoritmo propuesto se tomaron 30 corridas independientes por instancia, y
se seleccionó la mejor solución, siguiendo la metodología empleada también por los
métodos con los cuales se está comparando el algoritmo propuesto. Para los resultados
de los métodos de referencias, se toman los reportados en sus respectivos artículos.
Discusión de resultados
En la Tabla 1 se puede observar que el algoritmo propuesto obtiene casi siempre un resultado igual
o mejor al obtenido por otros métodos de optimización. De las 64 instancias tomadas
para experimentación, el algoritmo propuesto solo obtuvo un resultado peor a los obtenidos
anteriormente (marcados con asterisco) y mejoró los resultados en 36 instancias, mostrando
la eficacia del algoritmo para balancear la línea de producción de manera adecuada
en este tipo de problemas.
Tabla 1
Comparación de los resultados obtenidos por el algoritmo propuesto contra otros publicados
para los problemas de prueba.
|
|
|
Zamzam y Ahmed (2021)
|
Roshan, Roshani, Roshani (2013)
|
Dimitriadis (2006)
|
Fattahi, Roshani y Roshani (2011)
|
Zamzam, Sadek, Afia y El-Kharbo (2015)
|
Algoritmo propuesto
|
|
|
CT
|
NW
|
NS
|
NW
|
NS
|
NW
|
NS
|
NW
|
NS
|
NW
|
NS
|
NW
|
NS
|
|
Merten (7)
|
6
|
-
|
-
|
6
|
3
|
6
|
6
|
6
|
3
|
6
|
3
|
6
|
3
|
|
7
|
-
|
-
|
5
|
3
|
5
|
5
|
5
|
5
|
5
|
3
|
5
|
3
|
|
8
|
-
|
-
|
5
|
3
|
5
|
5
|
5
|
3
|
5
|
3
|
5
|
3
|
|
10
|
-
|
-
|
3
|
3
|
3
|
3
|
4
|
3
|
3
|
3
|
3
|
2
|
|
15
|
-
|
-
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
|
18
|
-
|
-
|
2
|
1
|
2
|
2
|
2
|
1
|
2
|
1
|
2
|
1
|
|
Bowman (8)
|
17
|
-
|
-
|
5
|
5
|
-
|
-
|
5
|
5
|
5
|
5
|
5
|
3
|
|
20
|
-
|
-
|
5
|
4
|
5
|
5
|
5
|
4
|
5
|
4
|
4
|
2
|
|
21
|
-
|
-
|
5
|
4
|
-
|
-
|
5
|
4
|
5
|
4
|
4
|
2
|
|
24
|
-
|
-
|
4
|
4
|
-
|
-
|
4
|
4
|
4
|
4
|
4
|
2
|
|
28
|
-
|
-
|
3
|
2
|
-
|
-
|
3
|
2
|
3
|
2
|
3
|
2
|
|
31
|
-
|
-
|
3
|
2
|
-
|
-
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Jaeschke (9)
|
6
|
-
|
-
|
8
|
6
|
8
|
8
|
8
|
5
|
8
|
6
|
8
|
4
|
|
7
|
-
|
-
|
7
|
6
|
7
|
7
|
7
|
5
|
7
|
6
|
7
|
4
|
|
8
|
-
|
-
|
6
|
5
|
6
|
6
|
6
|
5
|
6
|
5
|
6
|
3
|
|
10
|
-
|
-
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
2
|
|
18
|
-
|
-
|
3
|
2
|
3
|
3
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Jackson (11)
|
7
|
-
|
-
|
8
|
6
|
8
|
7
|
9
|
5
|
8
|
6
|
7
|
4
|
|
9
|
-
|
-
|
6
|
4
|
6
|
5
|
6
|
4
|
6
|
4
|
6
|
3
|
|
10
|
-
|
-
|
5
|
4
|
6
|
6
|
5
|
4
|
5
|
4
|
5
|
3
|
|
13
|
-
|
-
|
4
|
3
|
4
|
4
|
4
|
3
|
4
|
3
|
4
|
2
|
|
14
|
-
|
-
|
4
|
3
|
4
|
4
|
4
|
3
|
4
|
3
|
4
|
2
|
|
21
|
-
|
-
|
3
|
2
|
3
|
3
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Mansor (11)
|
45
|
-
|
-
|
5
|
3
|
-
|
-
|
5
|
3
|
5
|
3
|
5
|
3
|
|
54
|
-
|
-
|
4
|
3
|
-
|
-
|
4
|
3
|
4
|
3
|
4
|
2
|
|
63
|
-
|
-
|
3
|
2
|
-
|
-
|
3
|
2
|
3
|
2
|
3
|
2
|
|
72
|
-
|
-
|
3
|
2
|
-
|
-
|
3
|
2
|
3
|
2
|
3
|
2
|
|
81
|
-
|
-
|
3
|
2
|
-
|
-
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Mitchell (21)
|
14
|
-
|
-
|
8
|
7
|
9
|
9
|
8
|
7
|
8
|
7
|
8
|
4
|
|
15
|
-
|
-
|
8
|
7
|
8
|
8
|
8
|
7
|
8
|
7
|
8
|
4
|
|
21
|
-
|
-
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
3
|
|
26
|
-
|
-
|
5
|
4
|
5
|
5
|
5
|
4
|
5
|
4
|
5
|
3
|
|
35
|
-
|
-
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
2
|
|
39
|
-
|
-
|
3
|
2
|
3
|
3
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Heskia (28)
|
138
|
8
|
5
|
8
|
5
|
8
|
6
|
8
|
4
|
8
|
5
|
8
|
4
|
|
205
|
5
|
4
|
5
|
4
|
6
|
6
|
5
|
3
|
5
|
3
|
6
|
3
|
|
216
|
5
|
3
|
5
|
3
|
5
|
4
|
5
|
3
|
5
|
3
|
5
|
3
|
|
256
|
4
|
3
|
5
|
3
|
5
|
5
|
4
|
3
|
4
|
3
|
4
|
2
|
|
324
|
4
|
2
|
4
|
2
|
4
|
3
|
4
|
2
|
4
|
2
|
4
|
2
|
|
342
|
3
|
2
|
3
|
2
|
3
|
3
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Kilbridge (45)
|
57
|
10
|
6
|
10
|
6
|
10
|
8
|
10
|
5
|
10
|
6
|
10
|
5
|
|
79
|
7
|
4
|
8
|
4
|
7
|
6
|
7
|
5
|
7
|
5
|
8*
|
4*
|
|
92
|
6
|
4
|
7
|
4
|
6
|
5
|
7
|
4
|
6
|
4
|
6
|
3
|
|
110
|
6
|
3
|
6
|
3
|
6
|
5
|
6
|
3
|
6
|
3
|
6
|
3
|
|
138
|
4
|
3
|
4
|
3
|
4
|
4
|
4
|
3
|
4
|
3
|
4
|
2
|
|
184
|
3
|
2
|
3
|
2
|
3
|
3
|
3
|
2
|
3
|
2
|
3
|
2
|
|
Tonge (70)
|
176
|
21
|
17
|
21
|
19
|
22
|
21
|
21
|
14
|
21
|
19
|
21
|
11
|
|
364
|
10
|
6
|
10
|
7
|
10
|
9
|
10
|
5
|
10
|
7
|
10
|
5
|
|
410
|
9
|
5
|
9
|
5
|
9
|
7
|
9
|
4
|
9
|
5
|
9
|
5
|
|
468
|
8
|
4
|
8
|
4
|
8
|
7
|
8
|
4
|
8
|
4
|
8
|
4
|
|
527
|
7
|
4
|
7
|
4
|
7
|
7
|
7
|
4
|
7
|
4
|
7
|
4
|
|
Arcus (83)
|
5048
|
16
|
11
|
16
|
11
|
16
|
16
|
16
|
11
|
16
|
11
|
16
|
8
|
|
5853
|
14
|
10
|
14
|
10
|
14
|
13
|
14
|
10
|
14
|
9
|
14
|
7
|
|
6842
|
13
|
8
|
12
|
8
|
12
|
10
|
12
|
8
|
12
|
8
|
12
|
6
|
|
7571
|
11
|
9
|
11
|
10
|
11
|
11
|
11
|
7
|
11
|
7
|
11
|
6
|
|
8412
|
10
|
8
|
10
|
8
|
10
|
10
|
10
|
6
|
10
|
6
|
10
|
5
|
|
8998
|
10
|
5
|
9
|
7
|
9
|
8
|
9
|
6
|
9
|
6
|
9
|
5
|
|
10816
|
8
|
6
|
8
|
5
|
8
|
8
|
8
|
6
|
8
|
5
|
8
|
4
|
|
Arcus (111)
|
5755
|
-
|
-
|
-
|
-
|
27
|
24
|
27
|
14
|
27
|
21
|
27
|
14
|
|
8847
|
18
|
12
|
18
|
14
|
18
|
18
|
18
|
12
|
18
|
12
|
18
|
9
|
|
10027
|
16
|
10
|
16
|
12
|
16
|
15
|
16
|
10
|
16
|
11
|
16
|
8
|
|
10743
|
15
|
14
|
15
|
14
|
15
|
14
|
15
|
10
|
15
|
10
|
15
|
8
|
|
11378
|
14
|
8
|
14
|
9
|
14
|
9
|
14
|
7
|
14
|
9
|
14
|
7
|
|
17067
|
9
|
5
|
9
|
7
|
9
|
7
|
9
|
5
|
9
|
6
|
9
|
5
|
La Figura 6 nos permite identificar el valor esperado de las estaciones de trabajo para 6 instancias,
esta nos muestra que en todas las instancias el promedio de este indicador es menor
a los promedios presentados por Dimitriadis (2006); Fattahi, Roshani y Roshani (2011); Roshani, Roshani, Roshani (2013); Zamzam y Ahmed (2021). Los resultados son apropiados debido a que una de las funciones objetivo consiste
en la minimización de las estaciones de trabajo.
Figura 6
Número de estaciones promedio por algoritmo para los problemas Merten a Mitchell.
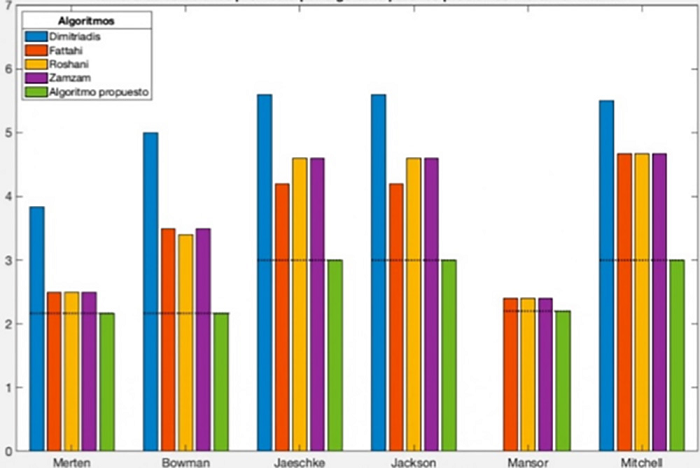
Fuente: Elaboración propia.
Por otra parte, el número promedio de estaciones de trabajo para las instancias Heskia,
Kilbridge, Tonge, Arcus y Arcus-2 es mejor para el algoritmo propuesto en este trabajo
en comparación con los propuestos por Zamzam y Ahmed (2021); Roshani, Roshani, Roshani (2013); Dimitriadis (2006); Fattahi, Roshani y Roshani (2011); Roshani y Giglio (2020); Zamzam, Sadek, Afia y El-Kharbotly (2015). Como se puede observar en la Figura 7 en todos los casos, el valor esperado de estaciones de trabajo es menor para el algoritmo
propuesto en este documento.
Figura 7
Número de estaciones promedio por algoritmo para los problemas Heskia a Arcus-2.
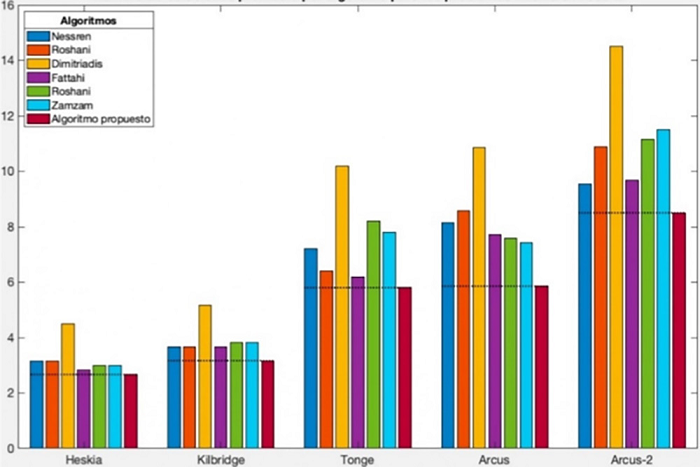
Fuente: Elaboración propia.
Como se mencionó en la sección denominada presentación de la problemática; uno de
los objetivos del problema planteado consiste en asignar tareas a los trabajadores
y a su vez a las estaciones de trabajo. Para representar la asignación se ilustra
la Figura 8, la cual contiene los diagramas de Gantt para la instancia Mitchell con un tiempo
de ciclo de 14 unidades. La Figura 8.A muestra los resultados de la asignación de tareas a los trabajadores para el operador
genético de selección. La Figura 8.B ilustra los resultados de la asignación al aplicar además de la selección el operador
genético denominado cruza, evidenciando una mejora en los resultados. Finalmente,
se muestran los resultados del operador genético mutación en el cual, previamente,
se procesaron los operadores selección y cruza, como se puede observar en la Figura 8.C. Este último operador genético tiene la intención de evitar óptimos locales.
Figura 8
Diagramas de Gantt de los trabajadores.
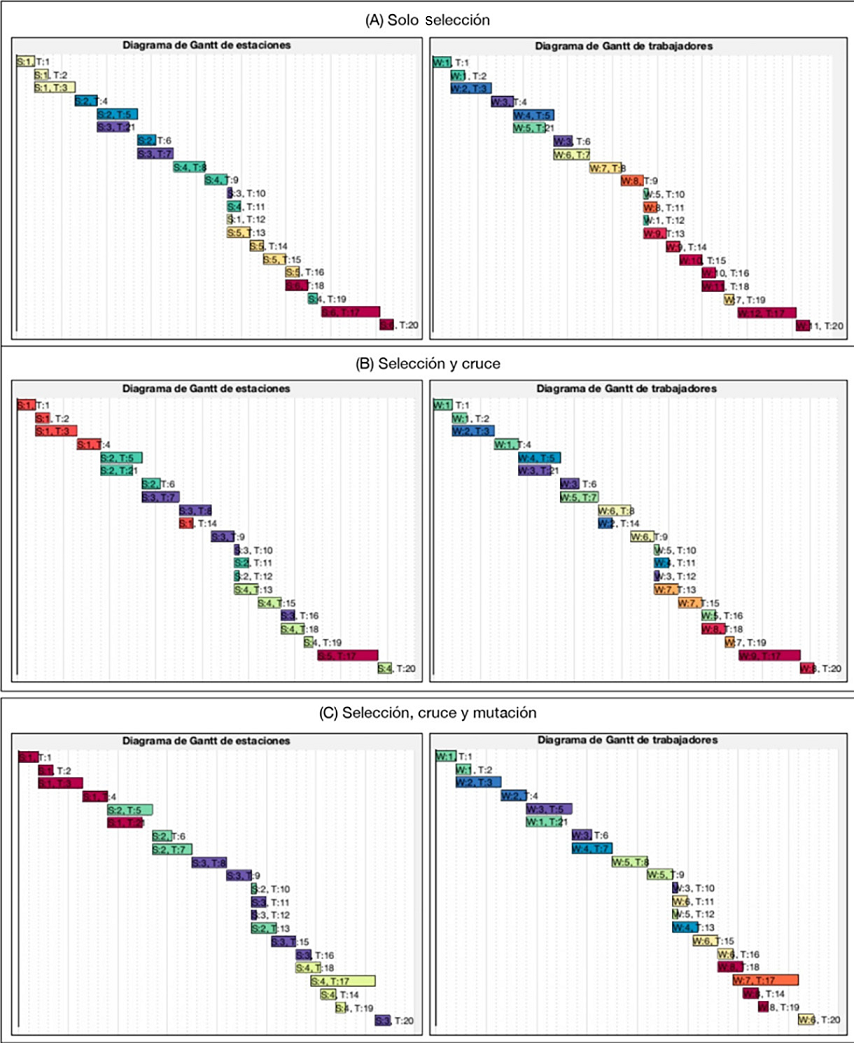
Fuente: Elaboración propia.
Para analizar los resultados obtenidos y compararlos respecto a la literatura, los
métodos comparados son: algoritmos genéticos (Zamzam y Ahmed 2021); recocido simulado (Roshani, Roshani, Roshani 2013); heurístico de agrupación denominado GM (Dimitriadis 2006); modelo matemático y optimización de colonia de hormigas (Fattahi, Roshani y Roshani 2011); algoritmos genéticos (Zamzam, Sadek, Afia y El-Kharbotly 2015), y el algoritmo propuesto en el presente documento. Se utilizó la prueba estadística
no paramétrica de Friedman; la cual se justifica debido a que el tamaño de las observaciones
es menor de 10; además, no se ajusta a una distribución de probabilidad normal. En
las pruebas estadísticas se utilizó el software especializado Minitab 21.3.0. Las pruebas se realizaron para cada una de las instancias
analizadas mediante el método del valor P con un nivel de significancia de 0.05 encontrando
lo siguiente:
La instancia Merten (7) se probó con los algoritmos propuestos por Dimitriadis (2006), Fattahi, Roshani y Roshani (2011), Roshani, Roshani, Roshani (2013), Zamzam, Sadek, Afia y El-Kharbotly (2015) y el algoritmo propuesto en este documento. El valor P para el método ajustado para
empates resultó ser de 0.003; la prueba es unilateral de orden inferior con un nivel
de significancia de 0.05, por lo cual la hipótesis nula no se acepta, es decir, las
medianas no son iguales como se puede observar en la Figura 9. Adicionalmente, se observa que la mediana del algoritmo propuesto es menor a la
de Dimitriadis (2006).
Figura 9
Resultados de la prueba de Friedman para la instancia Merten (7).

Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
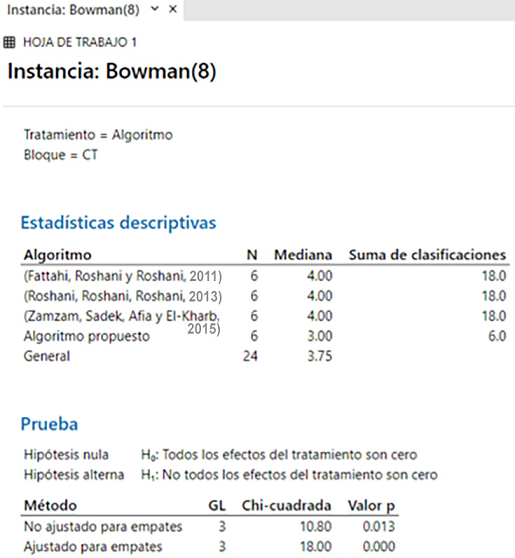
También se compararon los resultados de la instancia Bowman (8); la menor mediana
resultó ser la del método propuesto en el presente documento, en comparación con las
instancias: Dimitriadis (2006); Fattahi, Roshani y Roshani (2011); Roshani, Roshani, Roshani (2013); Zamzam, Sadek, Afia y El-Kharbotly (2015). La Figura 10 muestra que el valor P obtenido por la prueba de Friedman es 0.000, con el nivel
de signifiancia de 0.05 la hipótesis nula no se acepta; existe una diferencia significativa
entre las medias de los métodos evaluados, y, dado que la menor media resultó ser
la del algoritmo propuesto, se demuestra estadísticamente que este generó los mejores
resultados.
Figura 10
Resultados de la prueba de Friedman para la instancia Bowman (8).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
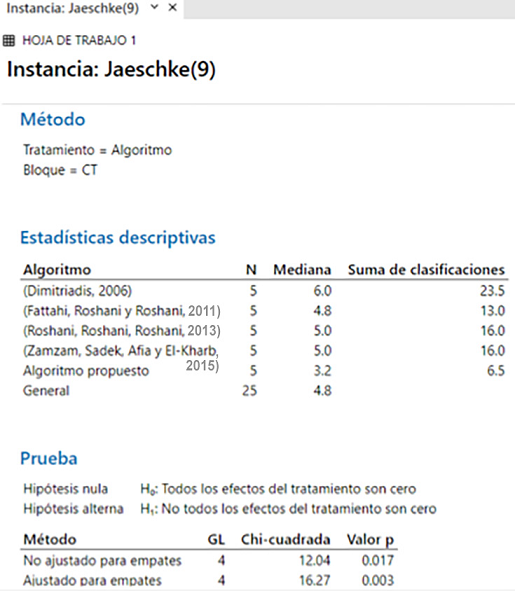
Por otra parte, se evalúo la instancia Jaeschke (9) respecto a los métodos mostrados
en la Figura 11. Es posible observar que el valor P es de 0.003. Al no aceptarse la hipótesis nula,
el mejor resultado es el que presenta la menor mediana, es decir, la del método propuesto
con 3.2.
Figura 11
Resultados de la prueba de Friedman para la instancia Jaeschke (9).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
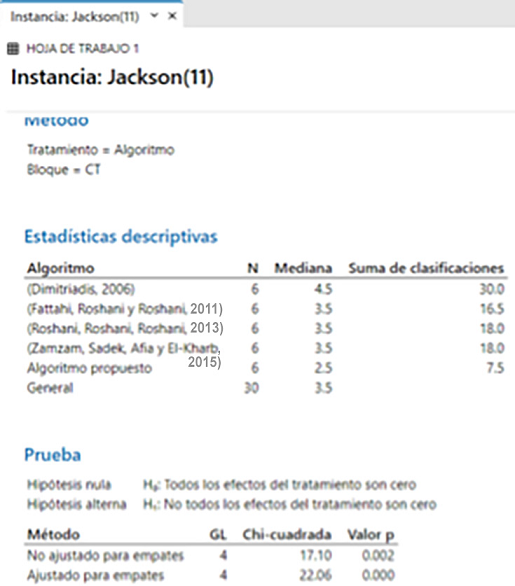
La instancia Jackson (11) se utilizó para comparar las instancias mostradas en la
Figura 12. Esta muestra como resultado de la prueba de hipótesis un valor P de 0.000 no aceptando
a la hipótesis nula, por lo cual existe una diferencia significativa. Adicionalmente,
la mediana del algoritmo propuesto es de 2.5, siendo el menor de los algoritmos comparados;
esta evidencia permite concluir que es el mejor método para la instancia evaluada.
Figura 12
Resultados de la prueba de Friedman para la instancia Jackson (11).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
Adicionalmente, se compararon las instancias Fattahi, Roshani y Roshani (2011); Roshani, Roshani, Roshani (2013); Zamzam, Sadek, Afia y El-Kharbotly (2015) con el algoritmo propuesto. Los resultados mostrados en la Figura 13 indican que no existe una diferencia significativa entre los métodos utilizados.
Figura 13
Resultados de la prueba de Friedman para la instancia Mansor (11).

Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
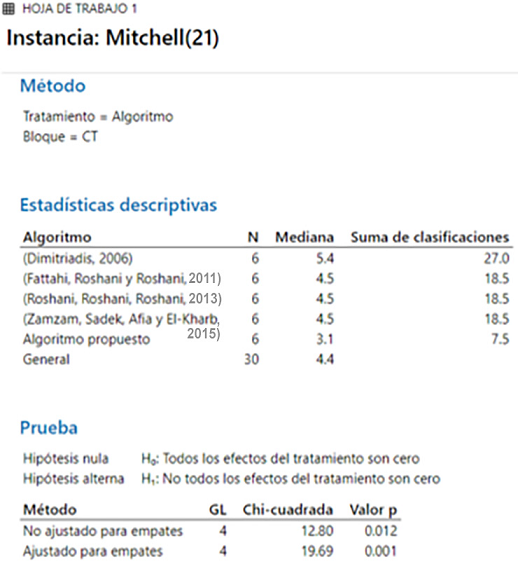
La instancia Mitchell (21) fue comparada con los algoritmos mostrados en la Figura 14; la hipótesis nula no se acepta en el nivel de significancia de 0.05, por lo cual
las medianas son diferentes, siendo el algoritmo propuesto la menor con 3.1.
Figura 14
Resultados de la prueba de Friedman para la instancia Mitchell (21).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
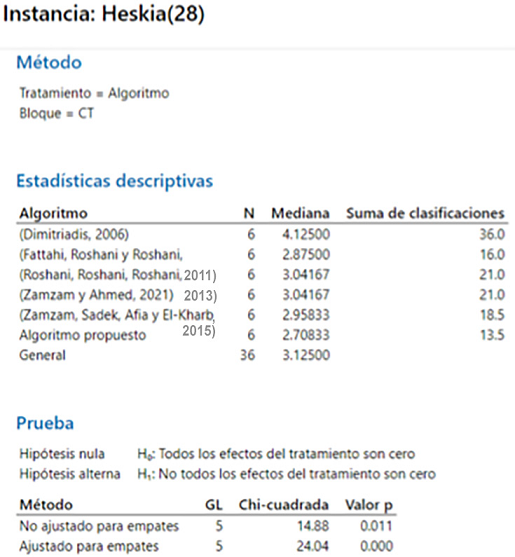
En la Figura 15 se muestras muestran los resultados de la prueba de Friedman para la instancia Heskia
(28), los cuales indican que el mejor resultado se presenta con el algoritmo propuesto,
esto debido a que la hipótesis nula no se acepta.
Figura 15
Resultados de la prueba de Friedman para la instancia Heskia (28).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
En la instancia Kilbridge (45) la hipótesis nula de la prueba de Friedman no se acepta,
debido a que el valor P es 0.000 y al tratarse de una prueba unilateral de cola izquierda
con un valor de 2.8 para la mediana, se observa que el algoritmo propuesto brinda
el menor número de estaciones de trabajo como se observa en la Figura 16.
Figura 16
Resultados de la prueba de Friedman para la instancia Kilbridge (45).

Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
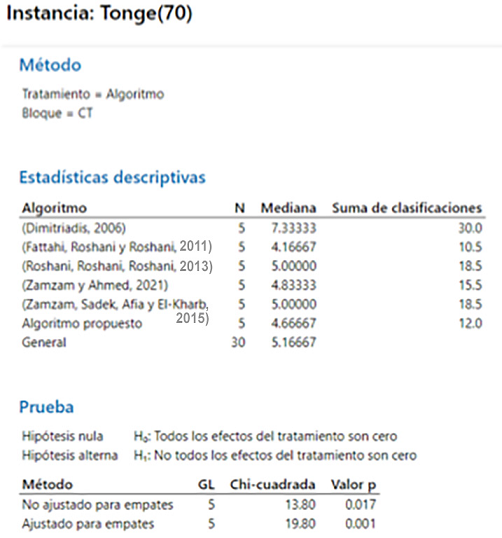
Para la instancia Tonge (70) se obtiene un valor P de 0.001 lo que cual no permite
aceptar la hipótesis nula. Esta información en conjunto con el valor de la media de
4.6 nos permite reconocer que el método propuesto es mejor al de Dimitriadis (2006); sin embargo, no existe diferencia significativa en relación con el resto de los
algoritmos de la literatura mostrados en la Figura 17.
Figura 17
Resultados de la prueba de Friedman para la instancia Tonge (70).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
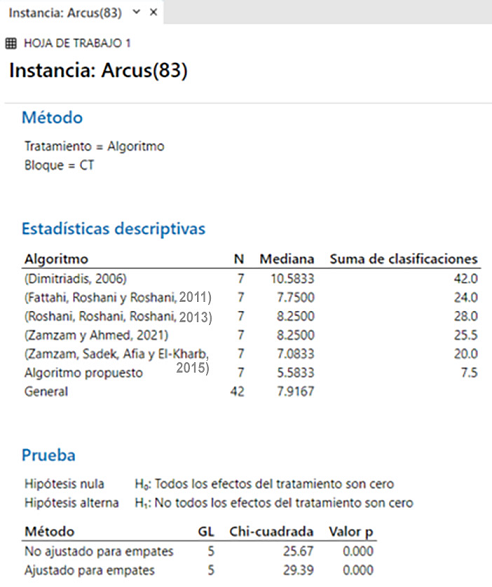
Para la instancia de Arcus (83) se compararon los algoritmos indicados en la Figura 18. La hipótesis nula no se acepta, teniendo como menor media el algoritmo propuesto.
Lo anterior implica que este método proporciona el menor número de estaciones de trabajo
para esta instancia.
Figura 18
Resultados de la prueba de Friedman para la instancia Arcus (83).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
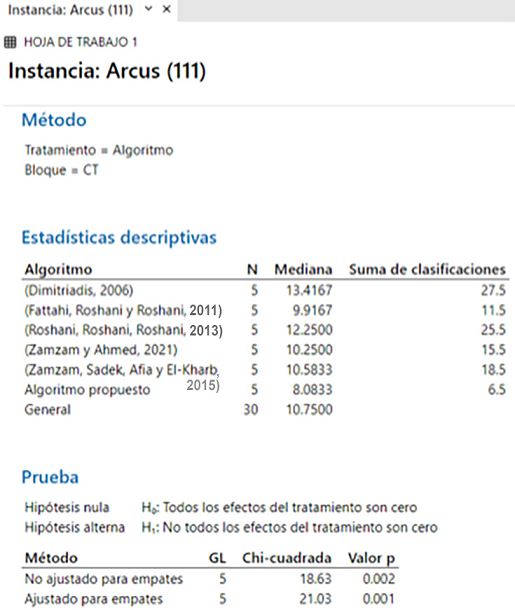
Finalmente, la instancia Arcus (111) se utilizó para comparar los algoritmos mostrados
en la Figura 19. Los resultados demuestran una diferencia significativa en las medianas; con el mínimo
de estas brindadas por el algoritmo propuesto.
Figura 19
Resultados de la prueba de Friedman para la instancia Arcus (111).
Fuente: Elaboración propia utilizando el software Minitab 21.3.0.
Conclusiones
En este trabajo se presentó un nuevo algoritmo genético para la optimización del número
de trabajadores y de estaciones de trabajo en una línea de ensamble multi-tripulada.
El algoritmo genético propuesto se caracteriza por castigar tiempos muertos altos
en la función costo, aplicar el cruce JBX para el refinamiento de nuevas soluciones
y no utilizar una política de rebalanceo fija, sino dejar este proceso al propio algoritmo
genético para la generación de mejores soluciones.
Se tomaron 11 tipos de problemas de prueba y un total de 64 instancias para comparar
el algoritmo propuesto con otros 6 métodos recientemente publicados, obteniendo resultados
satisfactorios y mejorando en 36 de estas instancias.
En el apartado “Discusión de resultados” se pueden observar las 11 instancias evaluadas
mediante la prueba de Friedman: en 10 instancias se mejoraron los resultados y en
una instancia no se mejoró. Lo anterior nos permite reconocer estadísticamente que
el algoritmo propuesto en el presente documento es factible y brinda mejores resultados
respecto al número de estaciones de trabajo requeridas para la producción.
El algoritmo propuesto en este manuscrito es fácil de implementar, y no utiliza ninguna
heurística de rebalanceo, sino que esta tarea la deja a los operadores genéticos del
algoritmo, lo cual le da mayor versatilidad y disminuye el procesamiento requerido
para refinar soluciones.
Por otra parte, el algoritmo maneja las variables de interés a optimizar con la linealización
de una función costo, y una ponderación para cada parte de esta (número de estaciones,
número de trabajadores y tiempos muertos). Un trabajo futuro propuesto es manejar
estas variables utilizando técnicas multi-objetivo, basadas en frente de Pareto y
dominancia de soluciones.
Otro trabajo futuro es darle más flexibilidad a la línea multi-tripulada para que
un trabajador pueda desarrollar su labor en varias estaciones de trabajo contiguas.
Esto requiere de la redefinición de la función costo y sus restricciones, lo cual
puede ser de interés en futuras investigaciones.
Por último, se propone analizar otras metaheurísticas híbridas de optimización basadas
en la inteligencia de enjambre que permitan una mayor flexibilidad entre las acciones
de exploración y explotación para el cálculo de soluciones.

